CFD算法库/免费代码

Warning

从2025年9月开始，每一次的LCO零基础CFD算法编程课，将会从下面的CFD算法文章库中进行筛选，并在课堂上现场介绍并植入。

下面标注号✰的算法，拍脑袋来讲，对于一个普通博士生来说（CFD从业4-5年），植入需要2个月左右，大概率可能3-4个月也不能收敛。对于一个博士后来说（CFD从业6-7年），植入且收敛需要最少2-3周左右。如果不收敛，CFD博士后能力不达标。对于CFD初学者，从开始学习到植入成功，应该按年计。

岳子的算法编程课，就是让你在 5天时间里面，把算法梳理清楚，同时进行植入。还不是一个求解器，是多个算法！

Note

LCO零基础CFD算法编程课不会介绍类似这种的课程要点：volScalarField的使用，geometricField的使用，Time类型，静态函数虚拟化函数，库文件结构...等。这不是我的风格。岳子只是告诉你我们要植入这些算法，你自然而然会学到相应的编程技巧。

音速与低速流全域求解器✰

OpenFOAM中现存的速度压力耦合算法主要是SIMPLE/PISO系列。历史上还存在各种变种。CFD算法编程课有一个必讲内容就是植入瞬态投影法、植入超音速求解器。这些是每次的基本内容。如果进一步向可压缩领域，OpenFOAM同样可以用来求解气动噪声。在一些情况下，声场中的压力可以看做一种小扰动。反过来，对于流体存在一种弱可压缩的连续介质，其中密度与压力的关系是线性变化的。在这种情况下，气动噪声的模拟不需要考虑温度方程，弱可压缩流体的模拟也不需要考虑温度方程，但同样也可以预测压力波的传递。该算法的强项在于其不仅可以预测通过音速传递的压力波，还可以预测低速流场结构。该算法主要调用的模型为以及正压法则：

\[ \rho^{t+\dt} =\rho^t+\frac{p^{t+\dt}-p^t}{c^2} \]

其中\(c\)表示音速。将该方程在OpenFOAM中植入看起来是有意思的并且可以帮助理解速度压力耦合的策略。该算法可以模拟音速传播的声场，且同时可以模拟低速流。注意：该求解器存在两个特征时间，一个是音速传输特征时间尺度，一个是流场的特征时间尺度。

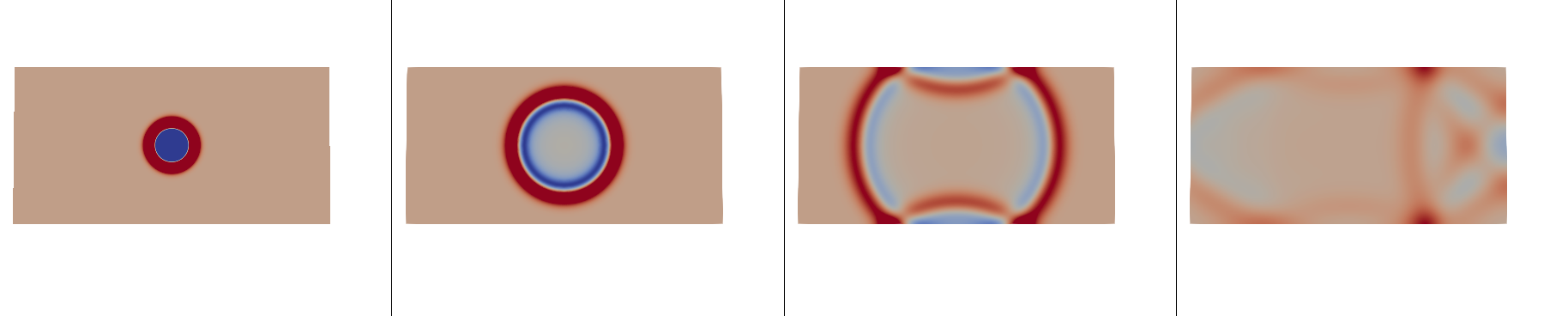
上图中是模拟的声场传播，左侧为无反射边界条件，很明显在第4个图中压力很好的传输出去。下图是用同样的求解器模拟的pitzDaily测试算例的低速流（速度10米每秒）密度场。在该求解器中如果添加噪声源（也可以人工通过setFields进行添加一次性的初始声源），可以很简单的求解低速流场中的气动噪声。

大统一的流体固体控制方程✰

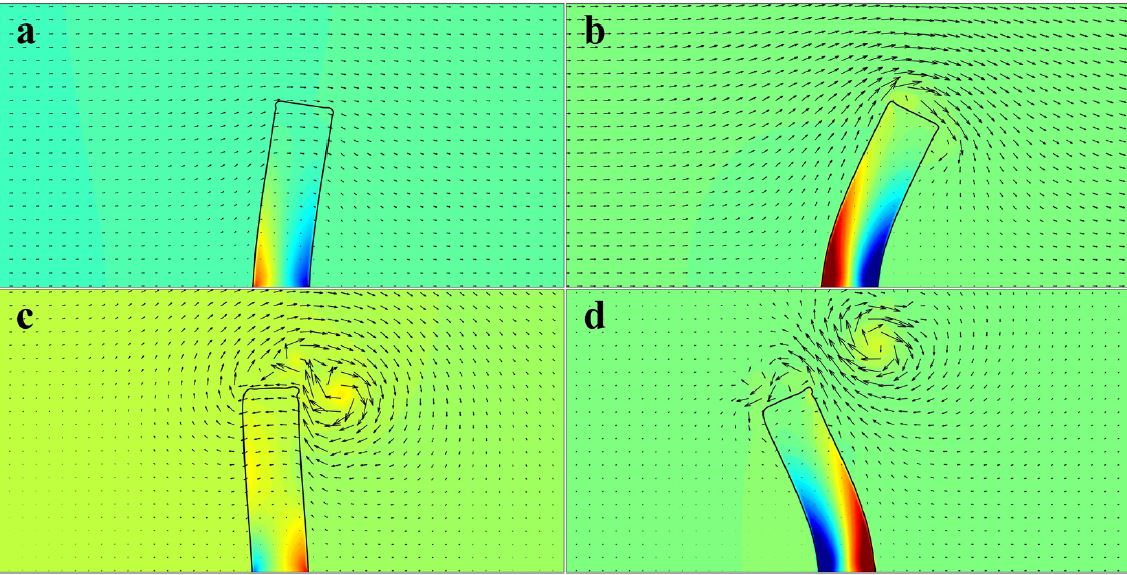
目前的流固耦合问题，都是在流体域求解NS方程，固体计算域求解固体方程。两套网格、两套PDE，在边界处进行耦合求解。如果能将流体与固体的控制方程写成大统一的形式，是否可以在一套网格上同时进行流固耦合的求解？在2020年刊发在JCP的一篇文章中[YK20]，开创性的将流体固体处理成大统一的控制方程，这样只需要求解一套速度方程，就可以同时获得流体计算域的速度，固体计算域的位移。理论上，针对线弹性固体，存在线弹性控制方程以及边界条件：

\[ \frac{\p ^2 \bfD}{\p t ^2}-\nabla\cdot\left( \mu(\nabla \bfD+\nabla \bfD^T) \right) + \nabla\cdot\left(\lambda (\nabla\cdot\bfD)\bfI \right)=0 \]

\[ \nabla\bfD \cdot\bfn = \frac{ \mathbf{T} +(2\mu+\lambda)\nabla\bfD \cdot\bfn - \boldsymbol{\sigma} \cdot\bfn }{2\mu+\lambda} \]

问题是如何将其写成速度方程？固体方程不存在压力怎么办？如何考虑流体固体大统一模型的边界条件？另外，固体线弹性PDE的收敛性非常差，如何保证大统一模型的收敛性？提示，相关的方程植入可以参考CFD: 线弹性方程。其实在OpenFOAM中，存在原生的求解\(\bfD\)的方程。但目的是将其修改成速度的方程，并且进一步的处理成大统一的速度压力方程。

如何保证高时间精度同时加快计算效率？✰

该相关算法爆了大量JCP[AF20, ATF23, KS23, KSS21, LM91]。或者说该方面研究已经可以单分一块。不可压NS方程求解最耗费时间的是压力方程。常规有限体积法求解充其量获得的是空间二阶、时间一阶的瞬态结果。龙格库塔（RK）时间步推进可以获得关于时间的高精度结果。大名鼎鼎的Moin以及Le看起来最早做了相关的尝试并发表在1991年的JCP上[LM91]，全文非常短，引用文献只有6个。单多步的RK推进需要求解更多的压力方程导致效率低下。一些文章力图实现的就是在多步RK推进下，仅仅推进一次压力方程来增加计算速度[AF20]。在OpenFOAM中植入RK算法并提升计算效率，看起来非常简单并且可以用于各种不同的工况验证（多篇sci就这样水出来了）。

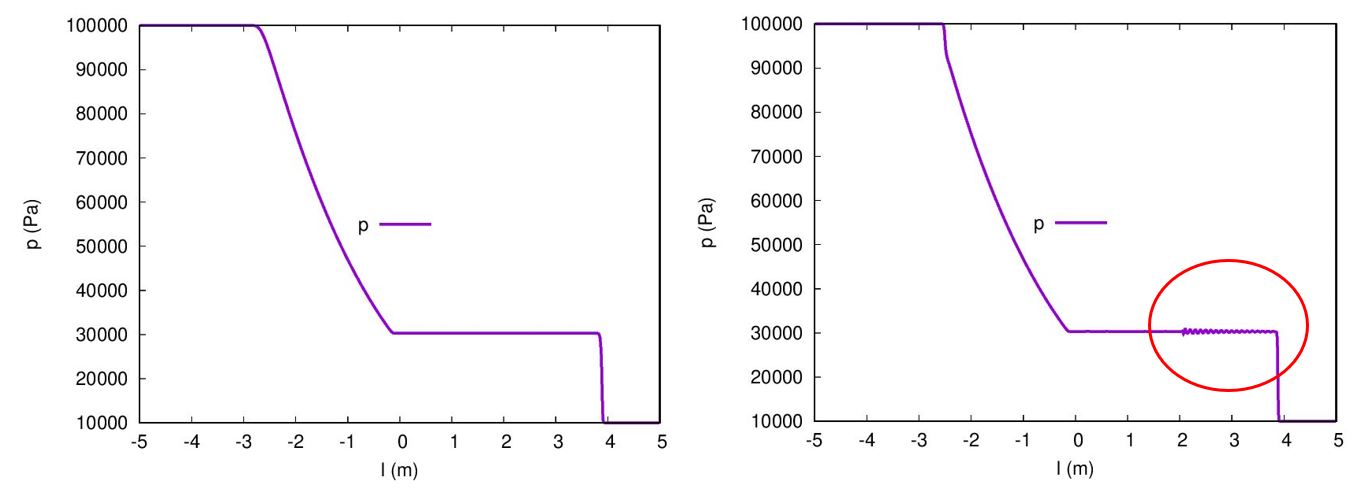
在练手阶段，植入瞬态投影法、稳态SIMPLE算法、普适性密度基可压缩算法是比较合适的。通过这些经典算法，你会透彻的了解NS方程速度压力耦合求解的思想。侧重算法的理解与编程。此部分内容是编程课的热身内容。3个求解器都是先从算法讲解开始，然后手搓求解器。另外，下图中红圈处会发现震荡。课堂上需要通过算法处理这个问题。

什么样的数值格式是动能守恒的？✰

考虑\(\frac{\p\frac{\phi^2}{2}}{\p t}\)，有：

\[ \frac{\p\frac{\phi^2}{2}}{\p t}=\phi\frac{\p\rho\phi}{\p t}+\frac{\phi^2}{2}\frac{\p\rho}{\p t} \]

将\(\frac{\p\rho\phi}{\p t}\)写为\(-\mathcal{C}\)，如果\(\frac{\p\rho\phi}{\p t}=-\mathcal{C}=-\nabla\cdot(\rho\phi\bfU)\)是成立的，同时定义中间变量\(\mathcal{M}\)：\(\frac{\p\rho}{\p t}=\mathcal{M}=-\nabla\cdot(\rho\bfU)\)，上式可以写为：

\[ \frac{\p\frac{\phi^2}{2}}{\p t}=- \left(\phi\mathcal{C} - \frac{\phi^2}{2}\mathcal{M}\right) \]

也即

\[ \frac{\p\frac{\phi^2}{2}}{\p t}=-\phi\nabla\cdot(\rho\phi\bfU) - \frac{\phi^2}{2} \nabla\cdot(\rho\bfU)=\nabla\cdot\left(\rho\frac{\phi^2}{2}\bfU\right) \]

这表明了如果\(\mathcal{C}\)和\(\mathcal{M}\)具有满足散度形式的方程，那么对于二次变量\(\phi^2\)也存在一个散度形式的守恒方程。这通常意味着整个系统是能量守恒的（\(\bfU^2\)能量相关）。相关的恒等关系在Coppola等发表在JCP的文章中被认为是二次变量恒等式[CCPdL19]。对于NS方程系统，所有的对流项都可以被认为是满足二次变量恒等（能量守恒）。但粘性项以及压力梯度项会导致能量的耗散。问题是，二次变量恒等在推导过程中，使用了散度的链条法则，这对于连续形式是没有问题的，但是在离散过程中并不适用。因此，对流项离散后往往不能保证二次变量恒等（能量守恒）。同样的，对于\(\mathcal{C}\)同样也具有不同的形式，例如其可以写为\(\nabla\cdot(\rho\phi\bfU)\)，也可以写成\(\phi\nabla\cdot(\rho\bfU)+\rho\bfU\cdot\nabla\phi\)。这里面牵涉的概念是使用什么样的变量形式去进行离散求解。Coppola等的文章中的公式7-11将其写成5种形式[CCPdL19]，并推导出满足能量守恒的系数法则。在后人的工作中被称之为动能守恒类方法（KEP）。Michele等在KEP方法基础之上进行改进，新的方法在2023年发表在JCP上[DMC23]。Ranocha等人在2022年发表文章，标题很有意思：如果你使用基于熵的高阶格式，即使压力不震荡，也不能解决局部不稳定问题[RG21]，也是基于该方法，对该方法进行植入并测试看起来是有意思的。

稀疏气固跨音速算法？✰

欧拉方程比较有意思，是因为欧拉方程存在间断。多维的欧拉方程求解存在激波，结果看起来也非常酷炫。在单相欧拉方程的基础上继续考虑颗粒，如果假定颗粒是稀疏的，变构成了跨音速的稀疏气固流动系统。在使用这一套方法用于经典激波管案例时候，变量的型线与单相欧拉方程存在区别[SMT03]：

进一步的考虑方程系统，有：

\[ \frac{\p \rho_g}{\p t}+\nabla\cdot(\rho_g\bfU_g)=0 \]

\[ \frac{\p \rho_g\bfU_g}{\p t}+\nabla\cdot(\rho_g\bfU_g\bfU_g + p)=-\frac{\rho_d}{m}\bfF_{drag} \]

\[ \frac{\p \rho_g E_g}{\p t}+\nabla\cdot( (\rho_g E_g + p)\bfU_g)=-\frac{\rho_d}{m} (Q+\bfU_d \cdot\bfF_{drag}) \]

\[ \frac{\p \rho_d}{\p t}+\nabla\cdot(\rho_d\bfU_d)=0 \]

\[ \frac{\p \rho_d\bfU_d}{\p t}+\nabla\cdot(\rho_d\bfU_d\bfU_d)=\frac{\rho_d}{m}\bfF_{drag} \]

\[ \frac{\p \rho_d E_d}{\p t}+\nabla\cdot( \rho_d E_d \bfU_d)=\frac{\rho_d}{m} (Q+\bfU_d \cdot\bfF_{drag}) \]

由于固相颗粒是稀疏的因此并不存在固相的压力。这个看起来很有意思因为稀疏气固激波管的流动型线看起来很特别，值得植入研究一下。

尝试写一个高精度、相场法的多相流求解器？✰

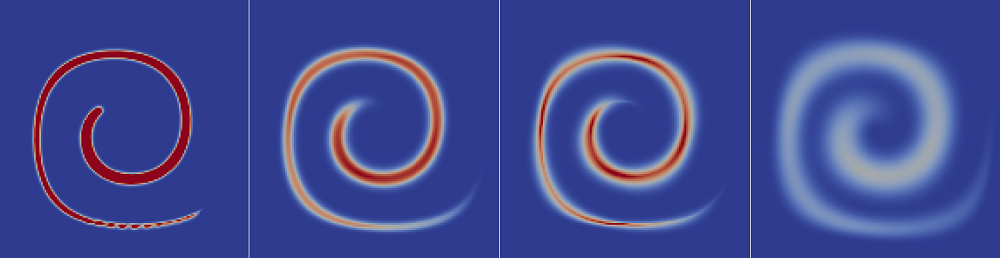
多相流的计算方法可以从NS方程进行简单的拓展。最简单的多相流计算方法就是直接模拟，在CFD领域，单相流的直接模拟也简单，因为不需要附加湍流模型。简单的模型的缺点就是比较贵。OpenFOAM目前显存了VOF方法。但植入一个新的方法看起来是有意思的，也比较适合练手。因此通过本算例植入的代码，主要研究1）相场法的思想、2）FVM的高精度格式、3）解的有界性、4）upwind与downwind等。如下图，采用不同的方法来计算zalesak disk的情况下，不同的格式会预测不同的结果。即使使用TVD格式也会产生数值耗散。对于普通的标量数值耗散并没有太大的问题。但某些情况下我们需要非常明晰的界面。这就需要不同的数值方法来处理。算法的难点在于：1）使用高精度算法如何保证有界性？2）如何保证界面的尖锐？3）不会产生一些奇怪的结果（如下图第三个，解的分布有点奇怪）。

随后，可以尝试句许植入一个两相流耦合求解器，算法主要考虑体积力对速度压力耦合的影响。CFD中的体积力有3种植入方式：1）隐性、2）显性、3）压力方程。可以对比不同的方法预测的结果。下面的结果就是计算出来的多相流不稳定性。经验来看，在入门CFD的过程中，很多人植入的算法都会发生数值震荡。

下面可以进一步的进行拓展。很明显上图的结果是比较耗散的。下一步可以尝试把两相流算法和高精度相场方法相结合，制定一个新的求解器。新的求解器求解后的结果如下图。可以很明显的看出求解的结果非常尖锐！在这个基础上，如果附加上表面张力，既可以形成一个全新的VOF求解器。

隐藏流体力学？

数据驱动CFD里面独树一帜的是PINN。通过PINN来练手看起来是个很好的选择，并且可以用来测试全连接网络、残差神经网络植入、以及新的激活函数等。使用PINN求解cavity flow的代码已经开源。不得不承认的是，PINN作为一个新兴的计算方法，用来计算流场实在是太慢了。因此使用PINN来计算流场，不像是走正常的套路。因此应该尝试将PINN用于正道，也即使用PINN来处理病态问题，用其处理经典CFD方法不能处理的问题，这个应该才是PINN真正的用处。这种应用也即之前刊发在Science正刊上的隐藏流体力学。否则用PINN来硬钢经典FVM，PINN必输无疑，太慢了，基本用不上。本案例的设计理念，就是把PINN用在正道上。在下图中，求解的ODE是未知的，但是PINN成功的发现了未知的ODE，并且数据与解析解完美吻合。

植入一个全新的湍流模型

从NASA收录的湍流模型来看，NASA认为最近10年能打的只有2个湍流模型，一个是2018年提出的代数应力模型k-kl，一个是2015年的Wray-Agarwal。2018年的代数应力模型引用少的可怜，应该是NASA自家的模型，因此被自家收录。因此，最近10年，能打的应该就是Wray-Agarwal湍流模型。把Wray-Agarwal湍流模型进行植入看起来挺有意思。相关的方程如下：

\[ S=\sqrt{2}|\bfS|, \bfS=\frac{\nabla\bfU+\nabla\bfU^T}{2}, W=\sqrt{2}|{\bf{W}}|, {\bf{W}}=\frac{\nabla\bfU-\nabla\bfU^T}{2} \]

\[ \eta=S \max\left(1, \left|\frac{W}{S}\right|\right) ,k=\frac{\nu_t S}{\sqrt{C_\mu}},\omega=\frac{S}{\sqrt{C_\mu}}, \]

\[ \mathrm{arg_1}=\frac{v+R}{2}\frac{\eta^2}{C_\mu k\omega},f_1=\mathrm{tanh}(\mathrm{arg_1}^4) \]

\[ C_1=f_1(C_{1kw} - C_{1k\varepsilon}) + C_{1k\varepsilon}, \sigma_R=f_1(\sigma_{kw}-\sigma_{k\varepsilon}) + \sigma_{k\varepsilon} \]

\[ C_{2kw}=\frac{C_{1kw}}{\kappa^2}+\sigma_{kw}, C_{2k\varepsilon}=\frac{C_{1k\varepsilon}}{\kappa^2}+\sigma_{k\varepsilon} \]

\[\begin{split} \begin{split} \frac{\p R}{\p t}+\nabla\cdot(\bfU R) &-\nabla\cdot((\sigma_R R+\nu)\nabla R)= \\\\ & C_1 R S + f_1 C_{2kw}\frac{R}{S}(\nabla R)\cdot(\nabla S)-(1-f_1)\min\left(C_{2ke}R^2 \frac{|\nabla S|^2}{S^2}, C_m|\nabla R|^2\right) \end{split} \end{split}\]

\[ \chi=R/v,f_\mu=\frac{\chi^3}{\chi^2+C_w^3},\nu_t= f_\mu R, \]

\[ \sigma_{kw}=0.72,\sigma_{k\varepsilon}=1.0,C_{1kw}=0.0829, C_{1k\varepsilon}=0.1284 \]

\[ \kappa=0.41,C_w=8.54,C_\mu=0.09, C_m=8.0 \]

植入数据驱动湍流模型✰

数据驱动湍流模型是目前国际的研究顶流。所有的课题组都对这个蠢蠢欲动。然而其实这是个非常简单的研究领域。如果说在OpenFOAM里面植入MULES算法可能需要一个博士，但植入数据驱动LES模型一个硕士生完全没问题。比如咱们进行的这个算例，采用经典神经网络架构，共训练2000个批次的数据，由于训练量比较小，使用CPU就可以进行训练。但是结果相当好。在下图中，数据驱动LES与经典CFD-LES预测的数据云图一致（局部差异基本可忽略）。在观测时间平均变量时候，结果非常完美。对于比较难预测的雷诺应力相关量，数据驱动LES预测的结果与经典CFD-LES吻合度非常高。类似的文章在2023年，2024年都刊发在了JFM。本算例的结果足以支撑一篇sci的数据。该算例部分代码开源在datadrivenles.md，该算例是以后LCO课程的教学案例。

数据驱动前沿热点

经典CFD经历了60多年的发展后，同位网格SIMPLE类算法在不可压缩领域统一江湖，可压缩领域通通都是密度基。数据驱动CFD目前的发展状况类似CFD在1970年代的情况，群魔乱舞百家齐放。目前还没有一个大统一的寡头算法出现。目前的态势是每家都有自己的特色，那么在10年后20年后数据驱动CFD，哪个算法会统一江湖目前还不确定。目前这一块研究的特色是杂！尤其在结合各种机器学习的网络后，更杂！但可以简单的进行归类。在《无痛苦NS方程笔记》里面，机器学习与CFD相应的结合点主要分为

流场重组（卷积网络、Unet、解码器、超分辨率、扩散模型与GAN）
求解加速（全连接网络、卷积网络、残差网络等）
数据驱动湍流模型（全连接网络、卷积网络、极限学习机等）
数据驱动多相流
循环神经网络与瞬态流场（循环神经网络、LSTM）
正向逆向PINN、隐藏流体力学
POD、DMD、流场降阶预测方法（不需要神经网络）
强化学习与过程控制

上述内容全部在《无痛苦NS方程笔记》里面有介绍，课堂上也会进一步的进行介绍。

数驱CFD免费代码

最终，在这里放出一些免费的数据驱动CFD的代码。岳子的课程定位是让大家自己在课堂写代码。但还是需要将两类代码免费放出，这些代码都是岳子自己亲自写的（岳子从来不在网上复制代码然后给你们）。这两类代码的特点是：

要么太简单，现场教学没啥意思；
要么太难，现场教学一教一个不吱声；

简单的代码现场教是拼凑内容。复杂的代码现场教大家消化不了。岳子注重教学效果、同时不拼凑教学内容。

参考文献

[AF20] (1,2)

Abhiram B Aithal and Antonino Ferrante. A fast pressure-correction method for incompressible flows over curved walls. Journal of Computational Physics, 421:109693, 2020.

[ATF23]

Abhiram B Aithal, Mira Tipirneni, and Antonino Ferrante. Temporal accuracy of fastrk3. Journal of Computational Physics, 475:111853, 2023.

[CCPdL19] (1,2)

Gennaro Coppola, Francesco Capuano, Sergio Pirozzoli, and Luigi de Luca. Numerically stable formulations of convective terms for turbulent compressible flows. Journal of Computational Physics, 382:86–104, 2019.

[DMC23]

Carlo De Michele and Gennaro Coppola. Asymptotically entropy-conservative and kinetic-energy preserving numerical fluxes for compressible euler equations. Journal of Computational Physics, 492:112439, 2023.

[KS23]

Mokbel Karam and Tony Saad. On the theory of fast projection methods for high-order navier-stokes solvers. Journal of Computational Physics, 495:112557, 2023.

[KSS21]

Mokbel Karam, James C Sutherland, and Tony Saad. Low-cost runge-kutta integrators for incompressible flow simulations. Journal of Computational Physics, 443:110518, 2021.

[LM91] (1,2)

Hung Le and Parviz Moin. An improvement of fractional step methods for the incompressible navier-stokes equations. Journal of computational physics, 92(2):369–379, 1991.

[RG21]

Hendrik Ranocha and Gregor J Gassner. Preventing pressure oscillations does not fix local linear stability issues of entropy-based split-form high-order schemes. Communications on Applied Mathematics and Computation, pages 1–24, 2021.

[SMT03]

Tsutomu Saito, M Marumoto, and K Takayama. Numerical investigations of shock waves in gas-particle mixtures: evaluation of numerical methods for dusty-gas shock wave phenomena. Shock Waves, 13(4):299–322, 2003.

[YK20]

H. Yeo and H. Ki. Unified momentum equation approach for fluid–structure interaction problems involving linear elastic structures. Journal of Computational Physics, 415:109482, 2020.