超音速问题相对于不可压缩流存在一些问题。如果考虑流场各处都是超音速的情况,也即双曲方程。流动信息全部从上游向下游进行传输,相对简单。但对于低音速的区域,流动特征既可以向上游也可以向下游传递。在二者混合的情况下,理想的通量格式,应该满足超音速与低音速俩种情况下的物理特征。即对于一个网格面,在超音速的情况下,从上游网格单元插值。对于低音速的情况下,从网格单元的两侧来获取插值。
HLL格式
在引入HLL格式之前。简单介绍几个背景问题:
own网格与nei网格:在有限体积法中,可以将网格面毗连的网格单元定义为这个面的own单元以及nei单元。每个内部面均存在own单元与nei单元。
网格体心值:定义在网格单元点上的值。考虑变量为\(\mathbf{W}\),网格体心值可以表示为\(\frac{1}{V}\int_{V}\mathbf{W}\rd V\)。
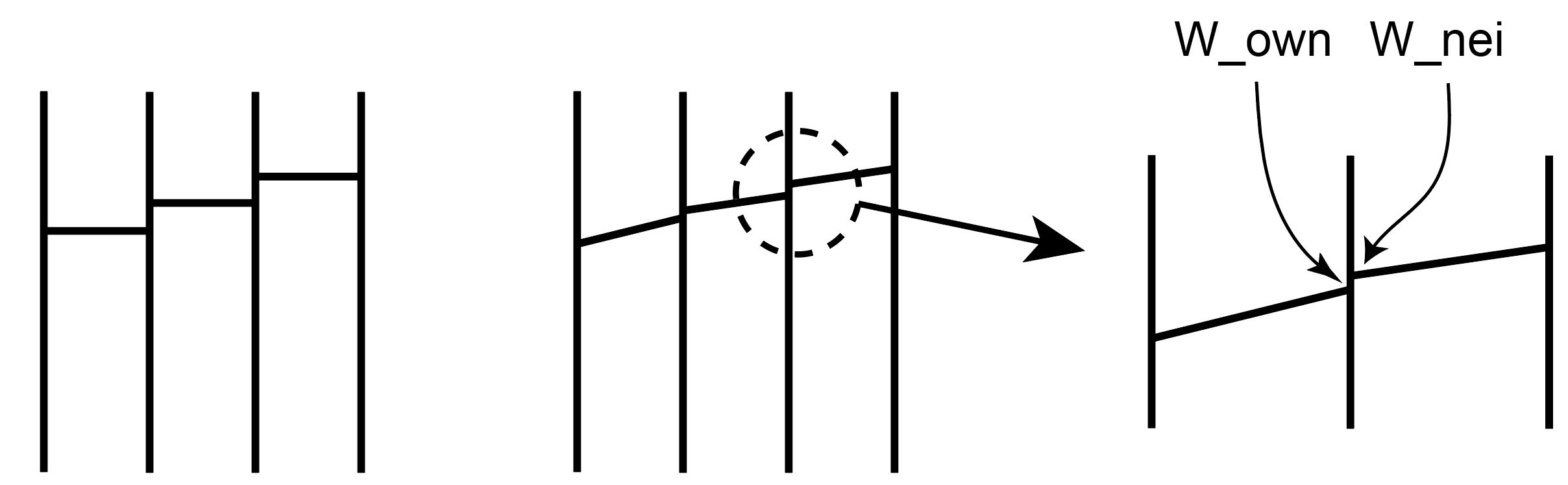
变量重组:这里区分为一阶以及高阶重组。考虑上图,在使用一阶格式的时候,网格内的各个位置的变量为均一的。考虑二阶格式,单一网格内不同位置的变量值不同,存在一个梯度。若使用更高阶的格式,图中的直线将会变成曲线。不管是一阶格式还是二阶格式,对于某个网格面上的值,均存在从不同的变量\(\mathbf{W}_{own}\)与\(\mathbf{W}_{nei}\)。
注意:
\(\bfW\)表示欧拉方程的守恒变量,例如\(\bfW_0=\rho\),\(\bfW_1=\rho\bfU\),\(\bfW_2=\rho E\)
波速计算:参考CFD: 可压 + 密度基,网格面上的传输通量的最大值与最小值,直接与own以及nei网格的影响区域相关。有:
(1)\[\begin{split}
ap_f=\max (\bfU_\own^f\cdot\bfS_f+c_\own^f|\bfS_f|, \bfU_\nei^f\cdot\bfS_f+c_\nei^f|\bfS_f|)
\\\\
am_f=\min (\bfU_\own^f\cdot\bfS_f-c_\own^f|\bfS_f|,\bfU_\nei^f\cdot\bfS_f-c_\nei^f|\bfS_f|)
\end{split}\]
在任何情况下,\(am_f\)都决定own网格影响区域的大小;在任何情况下,\(ap_f\)都决定nei网格影响区域的大小;如果\(am_f>0\),表示特征全部向nei网格传输;如果\(ap_f<0\),表示特征全部向own网格传输;
对于HLL格式,如果特征全部向一个方向传输,那么对于任意的\(\mathbf{W}_f\),其值取决于上游的网格体心值。在下面的内容中考虑另外一种情况,也即特征同时向own以及nei传播的情况。在这种情况下,必然后:
(2)\[\begin{split}
\begin{split}
am_f<0
\\
ap_f>0
\end{split}
\end{split}\]
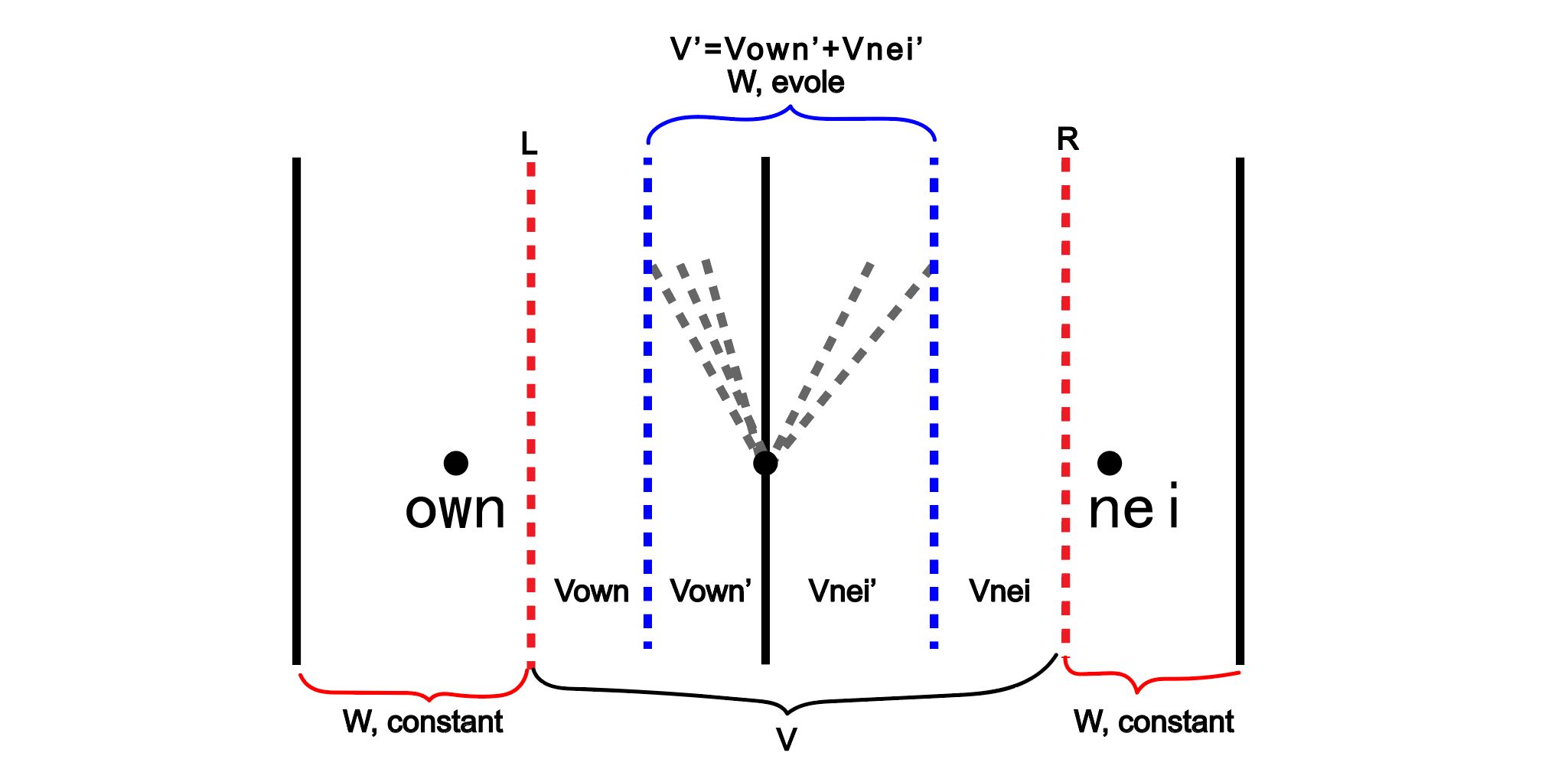
守恒法则:在下面的网格示意图中,黑线表示网格单元面,中间的黑线中的圆点表示面心,其中会存在黎曼问题。蓝色虚线包围的区域(W, evolve)表示影响区域,其中的\(\bfW\)的值会随着时间的推进而变化。对于时间步长比较小的情况下,影响区域仅仅存在于网格单元面的外围小区域。其他区域(W,constant)表示未受影响区域,其中的\(\bfW\)的值不会随着时间变化。现考虑红色虚线表示的网格,积分形式的守恒法则可以表示为:
(3)\[
\int_{V}\bfW^{t+\dt}\rd V=
\int_{V}\bfW^t\rd V
+\int_t^{t+\dt}F(\bfW_{own})\rd t - \int_t^{t+\dt}F(\bfW_{nei})\rd t
\]
方程(3)是精准的。同时,由于红色虚线位于未受影响区域,因此红色虚线上的通量并无变化。因此方程(3)可以简化为:
(4)\[
\int_{V}\bfW^{t+\dt}\rd V=
\bfW^t V
+\bigl(F(\bfW_{own}^t) - F(\bfW_{nei}^t)\bigr)\dt
\]
其中
(5)\[
\bfW^t V\approx\bfW_{own}^t (V_{own}+ V_{own}')+\bfW_{nei}^t (V_{nei}+ V_{nei}')
\]
即
(6)\[
\int_{V}\bfW^{t+\dt}\rd V=
\bfW_{own}^t (V_{own}+ V_{own}')+\bfW_{nei}^t (V_{nei}+ V_{nei}')
+\bigl(F(\bfW_{own}^t) - F(\bfW_{nei}^t)\bigr)\dt
\]
从另外的角度来看,\(\int_{V}\bfW^{t+\dt}\rd V\)可以分为三个区域:
(7)\[
\int_{V}\bfW^{t+\dt}\rd V=
\int_{V_{own}}\bfW^{t+\dt}\rd V
+\int_{V'}\bfW^{t+\dt}\rd V
+\int_{V_{nei}}\bfW^{t+\dt}\rd V
\]
再一次的,由于\(V_{own}\)以及\(V_{nei}\)区域为非影响区域,因此可以简化为:
(8)\[
\int_{V}\bfW^{t+\dt}\rd V=
V_{own}\bfW^{t}_{own}
+\int_{V'}\bfW^{t+\dt}\rd V
+V_{nei}\bfW^{t}_{nei}
\]
结合方程(8)与(6),有:
(9)\[
\int_{V'}\bfW^{t+\dt}\rd V
=
\bfW_{own}^t V_{own}'+\bfW_{nei}^t V_{nei}'
+\bigl(F(\bfW_{own}^t) - F(\bfW_{nei}^t)\bigr)\dt
\]
左右除以体积\(V'\)有:
(10)\[
\frac{1}{V'}\int_{V'}\bfW^{t+\dt}\rd V
=
\Bigl(\bfW_{own}^t V_{own}'+\bfW_{nei}^t V_{nei}'
+\bigl(F(\bfW_{own}^t) - F(\bfW_{nei}^t)\bigr)\dt\Bigr)\frac{1}{V'}
\]
\(\frac{1}{V'}\int_{V'}\bfW^{t+\dt}\rd V\)可以理解为\(V'\)控制体的平均的\(\bfW\)的值。在HLL方法中,\(\bfW\)被认为是\(\bfW_{hll}\)。进一步有:
(11)\[
\bfW_{hll}
=
\frac{\bfW_{own}^t V_{own}'+\bfW_{nei}^t V_{nei}'
+\bigl(F(\bfW_{own}^t) - F(\bfW_{nei}^t)\bigr)\dt}{V_{own}'+V_{nei}'}
\]
如果知道影响区域的体积\(V'\)的大小,\(\bfW_{hll}\)可解。依据上文最大波速的讨论,有
(12)\[
V_{nei}'\approx\Delta t|\bfS_f| ap_f,
V_{own}'\approx\Delta t|\bfS_f| (-am_f)
\]
Note
注意其中为\(-am_f\),因为\(am_f<0\)。
将其代入到方程(11)有:
(13)\[
\bfW_{hll}
=
\frac{\bfW_{nei}^t |\bfS_f| ap^f -\bfW_{own}^t |\bfS_f| am^f
+ F(\bfW_{own}^t) - F(\bfW_{nei}^t) }{|\bfS_f| (ap^f-am^f)}
\]
举例,如果考虑密度的话,有:
(14)\[
\rho_{hll}
=
\frac{\rho_{nei}^t ap^f - \rho_{own}^t am^f
+ \bfU_{own}\cdot\bfn_f\rho_{own}^t - \bfU_{nei}\cdot\bfn_f\rho_{nei}^t }{ ap^f - am^f}
\]
在这里要注意,\(\bfW_{hll}\)是对\(V'\)控制体做积分后,人为糅合后出现的一个值,其近似可以认为是在\(\dt\)时间间隔内的一种平均值。要获得精准的\(\int_t^{t+\dt}F(\bfW)\rd t\)通量函数,还需要进一步的进行计算。
现在单独考虑\(V_{nei}'\)体积,有:
(15)\[\begin{split}
\begin{multline}
\int_{V_{nei}'}\bfW^{t+\dt}\rd V
=
\int_{V_{nei}'}\bfW_{hll}\rd V
=
V_{nei}' \bfW_{hll}=
\\
\bfW^t_{nei} V_{nei}' + \int_{t}^{t+\dt}F(\bfW_{hll}) \rd t- \int_{t}^{t+\dt}F(\bfW_{nei}^t)\rd t=
\\
\bfW^t_{nei} V_{nei}' + F(\bfW_{hll}) \dt- F(\bfW_{nei}^t)\dt
\end{multline}
\end{split}\]
也即:
(16)\[
|\bfS_f| ap^f \bfW_{hll}=
\bfW^t_{nei} |\bfS_f| ap^f + F(\bfW_{hll}) - F(\bfW_{nei}^t)
\]
(17)\[
F(\bfW_{hll}) = F(\bfW_{nei}^t) + |\bfS_f| ap^f \left( \bfW_{hll} - \bfW^t_{nei} \right)
\]
将方程(13)代入到(17)有:
(18)\[
F(\bfW_{hll}) =
\frac{ am^fap^f \left(\bfW_{nei}^t |\bfS_f| -\bfW^t_{own}|\bfS_f|\right) + ap^fF(\bfW_{own}^t) - am^fF(\bfW_{nei}^t) }{ ap_f-am^f}
\]
AUSM格式
AUSM格式依据面网格的马赫数方向,来对通量进行区分。在可压缩领域,存在大量的矢通量格式、通量差分裂等格式。AUSM格式将压力与对流速度进行区分,理解相对更加简单。首先介绍几个背景概念:
音速\(c\):\(c=\sqrt{\gamma\frac{p}{\rho}}\)。马赫数标量\(|\bfM|\):\(\frac{|\bfU|}{c}\)。
马赫数矢量\(\bfM\): \(\bfU/c\),\(c\)表示音速。其中马赫数的分量表示速度各个方向的马赫数。
面马赫数\(M_f\): \(\frac{\bfU_f\cdot\bfS_f}{c |\bfS_f|}\),其为一个定义在网格面上的标量。其值的大小可以用来判断插值的方向。
首先将通量均通过马赫数来表示,其中面的速度,可以写成网格面马赫数的形式:
(19)\[
\bfU_f \cdot \bfS_f= c_f M_f |\bfS_f|
\]
进一步的有质量密度、动量密度、能量密度通量的对流项:
(20)\[
\bfW_f (\bfU_f \cdot \bfS_f)=\bfW_f(c_f M_f |\bfS_f|) =\bfW_f c_f |\bfS_f| M_f
\]
动量密度\(\bfW_1\)通量的压力项:
(21)\[
p_f\bfS_f=\frac{c_f^2}{\gamma_f}\rho_f\bfS_f
\]
能量密度\(\bfW_2\)通量压力对流项:
(22)\[
p_f\bfU_f \cdot \bfS_f= \frac{c_f^2}{\gamma_f}\rho_f(c_f M_f |\bfS_f|)
\]
AUSM分裂认为对于网格单元面,可以认为其影响区域取决于上下游。在超音速情况下,网格面信息全部来源于上游。亚音速情况下,网格面信息来自于左右两侧的网格单元。因此AUSM分裂将网格单元面的贡献依据特征值的大小,区分为左右网格单元(上下游)的贡献:
\(M_f\geqslant 1\):网格面的值全部来自于上游。
\(M_f\leqslant -1\):网格面的值全部来自于下游。
\(-1<M_f<1\):网格面的值来自于上下游的混合。
AUSM分裂认为:
(23)\[
M_f^+=\frac{1}{4}(M_f^++1)^2,M_f^-=-\frac{1}{4}(M_f^--1)^2
\]
(24)\[
M_f=M_f^+ + M_f^-
\]
注意:
其中\(^+,^-\)表示上下游。具体是own网格还是nei网格,可以通过通量的大小来判断。
方程(23)满足\(M\)为连续的、可导的、并且为低阶的。\(M_f\)用于判断信息的方向并进行插值。至此,AUSM中的关于速度通量的这部分的计算过程如下:
通过方程(24)来计算面马赫数;
依据面马赫数定义的方向,来更新面守恒变量的值\(\bfW_f\),\(c\)为定值;至此,方程(20)中的\(\bfW_f c_f |\bfS_f|\)可以更新;
结合方程(24)来更新方程(20)的\(\bfW_f c_f |\bfS_f| M_f \);
下面来看压力的贡献,AUSM格式认为方程变量中的对流与压力来自于不同的贡献,因此在处理通量的情况下,需要将对流贡献与压力贡献单独处理。AUSM格式将其写为:
(25)\[
p^+_f=\frac{1}{2}\frac{c_f^2}{\gamma_f}\rho_f^+(1+M^+),p^-_f=\frac{1}{2}\frac{c_f^2}{\gamma_f}\rho_f^-(1-M^-)
\]
(26)\[
p_f = \frac{c_f^2}{\gamma_f}\rho_f = p^+_f + p^-_f
\]
至此,AUSM中的关于压力通量的这部分的计算过程如下:
通过方程(26)来计算\(p_f\);
依据\(p_f\)方向,来更新方程(21)以及(22);