CFD: 多相VOF算法
VOF多相流方法可用于求解多相流的界面问题，如崩塌的堤坝、极少量的气泡界面、液体晃荡等。界面类存在两个关键问题：
界面尽可能要薄；
在界面失稳的情况下算法要尽可能的稳定；
本文从最基本的液膜压力降开始分析，一步一步推导VOF模型。对于大量气泡/液滴存在的情况，VOF模型对网格分辨率要求较高。在这种情况下可以使用多流体模型来计算。在有重力以及源项的情况下，有不可溶多相体系动量方程：
(1)\[
\frac{\partial \rho \mathbf{U}}{\partial t}+\nabla \cdot (\rho \mathbf{U} \mathbf{U} ) - \nabla \cdot \boldsymbol{\tau} =-\nabla p+\rho\bfg+\bfF
\]
其中各项的含义可参考CFD:不可压瞬态PISO算法，\(\bfF\)表示表面张力。连续性方程可以表示为
(2)\[
\frac{\partial \rho}{\partial t}+\nabla \cdot (\rho \mathbf{U})=0
\]
若考虑两种流体均为不可压缩的，也即考虑某种流体运动的流体微元，其密度\(\rho\)以及相分数随着\(\bfU\)进行推进，因此其物质导数为\(0\)，即
(3)\[\begin{split}
\frac{\rD \rho}{\rD t}=\frac{\partial \rho}{\partial t}+\bfU\cdot\nabla\rho=0
\\\\
\frac{\rD \alpha}{\rD t}=\frac{\partial \alpha}{\partial t}+\bfU\cdot\nabla\alpha=0
\end{split}\]
将方程(3)代入到(2)有：
(4)\[
\nabla\cdot\bfU=0
\]
在这种情况下，方程(1)和(4)组成了不可压缩多相界面类模型中关于速度和压力的方程。其中不同的相具有不同的密度。在速度\(\bfU\)已知的情况下，方程(3)中的密度为纯对流方程可以进行求解。在Front-tracking方法中，方程(3)并没有直接进行求解而是通过某种界面重组的方法进行组建。在Volume of fluid（VOF）方法中则定义了一个变量\(\alpha\)来表示流体的相分数。考虑某一个网格单元的气液两相系统，如果此网格单元内充满了流体，则\(\alpha=1\)；如果此网格单元内充满了气体，则则\(\alpha=0\)。如果\(\alpha\)的值介于\(0\)和\(1\)之间，则此网格单元内为气液混合。可见，CFD中VOF的界面是通过跟踪相分数来获得的，并不是直接算出来的，是通过计算每个网格内的相场值而后处理出来的。网格越密，VOF后处理出来的界面越薄。如下图所展示，VOF与Front-tracking这些模型均为界面重构的微观多相流模型。可以看作为多相计算流体力学领域的直接模拟。
表面张力模化
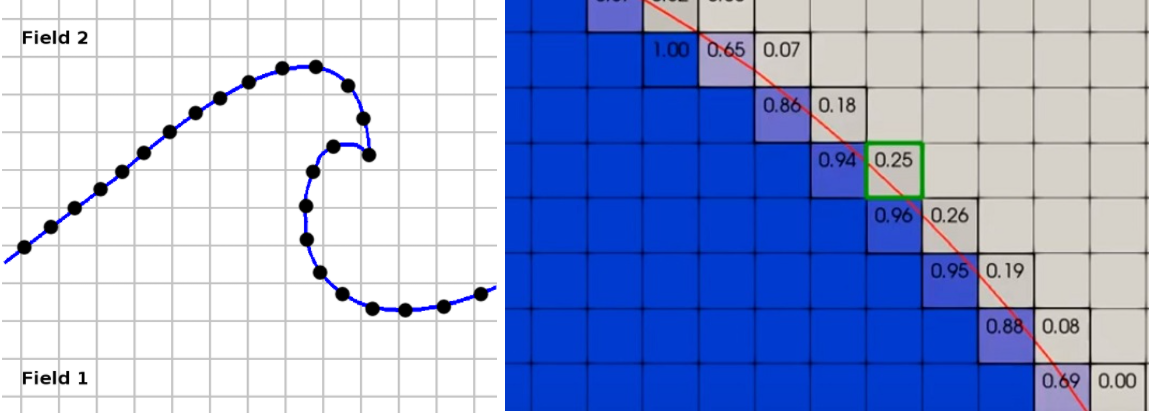
VOF方程在动量方程右侧存在一个表面张力项需要模化。表面张力最重要的特征即其会导致界面处存在一个尖锐的界面压力降\(\Delta p\)。考虑如图(1)所示的一个曲面微元。其中\(p_1\)为曲面微元上方空气向下施加的压强，\(p_2\)为曲面微元下方液体向上施加的压强，假想一个水中的圆形气泡，压力在气泡内要大于周围液体的压力。因此有压力降\(\Delta p =p_1-p_2\)。这个效应需要在动量方程中有所体现。定义表面张力为\(\bfF_\sigma\)，其是一种为了保持界面平衡而作用在每单位长度上的力，是一种和界面相切的张力。表面张力的大小主要和流体的物理特性有关。在曲面中，均衡的流体表面张力和压力降\(p_1-p_2\)均衡。图示中的压力降方向向下，因此界面张力的作用方向向上。这个界面压力降主要取决于表面张力和曲面弧度。下图即为两相界面处的曲面微元受力示意图。
图中\(s_1\)和\(s_2\)分别表示曲面微元的俩个边长。因此有曲面微元的面积为\(\rd s_1\rd s_2\)，曲面微元上的总压力的值为：
(5)\[
F_p=(p_1 - p_2) \mathrm{d}s_1 \mathrm{d}s_2
\]
方程(5)中的\(F_p\)为一个向下的力。基于表面张力的定义，其作用在曲面微元的四个边上，且合力向上和曲面微元上的总压力\(F_p\)均衡。如果表面张力系数定义为\(\sigma\)。那么作用在\(\mathrm{d}s_1\)上的表面张力为\(\sigma\mathrm{d}s_1\),其在\(y\)方向上的分量为：\(\sigma\mathrm{d}s_1 \mathrm{sin} \frac{\mathrm{d}\beta}{2} \approx \sigma\mathrm{d}s_1 \frac{\mathrm{d}\beta}{2} \)。同理，作用在\(\rd s_2\)上的\(y\)方向分量为\(\sigma\mathrm{d}s_2 \frac{\mathrm{d}\alpha}{2}\)。对四个边加和之后，有作用在曲面微元上的表面张力之和的大小为：
(6)\[
\begin{split}
F_\sigma&=\sigma(\rd s_1 \rd\beta+\rd s_2\rd\alpha)
=\sigma\left(\frac{\rd\beta}{\rd s_2}+\frac{\rd\alpha}{\rd s_1}\right)\rd s_1\rd s_2
\end{split}
\]
现用\(\bfn\)来表示曲面微元的单位法向，其从较高的相分数指向较低的相分数，其模为\(1\)。有
(7)\[
\frac{n_x|_{x+\Delta x/2}-n_x|_{x}}{\Delta x/2} \frac{|\Delta x|}{2}=\frac{\p n_x}{\p x} \frac{\rd x}{2}=
\mathrm{sin}\frac{\alpha}{2} \approx \frac{\rd \alpha}{2}
\]
也即：
(8)\[
\frac{\p n_x}{\partial x} = \frac{\mathrm{d}\alpha}{\mathrm{d} x} = \frac{1}{R_1}
\]
同理对于\(s_2\)方向有
(9)\[
\frac{\p n_y}{\partial y} = \frac{\mathrm{d}\beta}{\mathrm{d} y} = \frac{1}{R_2}
\]
对于纵向，\(n_z\)并无增量，因此
(10)\[
\frac{\p n_z}{\partial z} = 0
\]
其中\(R_1\)，\(R_2\)为图中\(\mathrm{d}s_1\)（也即\(\rd x\)），\(\mathrm{d}s_2\)的（也即\(\rd y\)）主曲率半径（单位为m）。将方程(8)、(9)带入到(6)有：
(11)\[
\begin{split}
F_\sigma
=\sigma\left( \frac{1}{R_1}+ \frac{1}{R_2} \right)\rd s_1\rd s_2
\end{split}
\]
综合\(\bfn\)导数的各个分量，有
(12)\[
\nabla \cdot \bfn = \frac{\partial \bfn}{\partial x} + \frac{\partial \bfn}{\partial y} + \frac{\partial \bfn}{\partial z} =\left( \frac{1}{R_1}+ \frac{1}{R_2} \right)
\]
即：
(13)\[
\begin{split}
F_\sigma
=\sigma\nabla\cdot\bfn\rd s_1\rd s_2
\end{split}
\]
均衡状态下有\(F_p = F_\sigma\)，结合方程(13)与(5)即：
(14)\[
\Delta p =p_1 - p_2=\sigma\left(\frac{1}{R_1}+\frac{1}{R_2} \right)= \sigma \nabla \cdot \bfn
\]
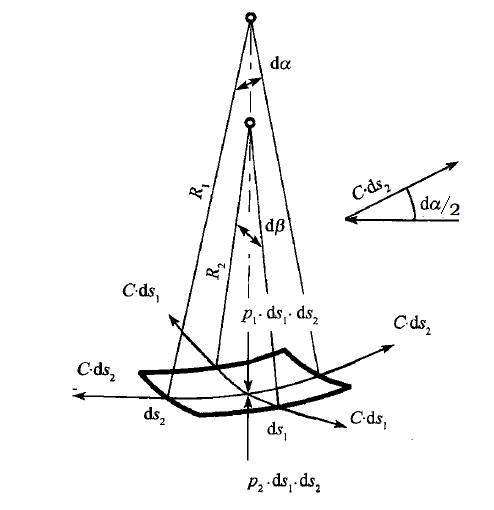
由于\(\bfn\)为一个未知量，因此需要进行封闭。如上图所示，对于CFD中的自由表面，某一点的法向量为\(\nabla\alpha\)，其为一个连续函数，在流体1和2区内部为0，仅仅在自由表面存在非零值。图(2)自由表面的单位法向量可表示为：
(15)\[
\bfn=\frac{\nabla \alpha}{|\nabla \alpha|}
\]
其中\(\nabla\alpha\)表示相分数的梯度，\(\nabla\alpha\)表示与相分数界面垂直的方向。这是因为\(\nabla\alpha\)的分量为\(\frac{\p\alpha}{\p x},\frac{\p\alpha}{\p y},\frac{\p\alpha}{\p z}\)，每个分量表示一个方向的梯度大小，这些矢量分量组合在一起就是与相界面垂直的方向矢量，具有明确的意义。在这种情况下有：
(16)\[
\Delta p = \sigma \nabla \cdot \left(\frac{\nabla \alpha}{|\nabla \alpha|}\right)
\]
方程(16)表示界面两端处的压力降，为一个间断函数，只适用于非常尖锐的界面，从物理上更倾向于是一个在界面处施加一个边界条件。在实际计算中，这种情况很难达到且难以实施。Continuum Surface Force模型可以较为容易的模化表面张力。参考上图，在界面处的\(y\)方向，CSF模型将间断压力降处理为一个连续函数：
(17)\[
p_b-p_a=\sigma \kappa(\alpha_b-\alpha_a)
\]
其中\(\kappa\)表示界面处的曲率，其大小为\(\nabla\cdot\bfn\)。由于在界面处\(p\)为一个增量函数，由于\(\alpha_b-\alpha_a\leqslant0\)，因此界面处的曲率为：
(18)\[
\kappa = - \nabla \cdot \bfn
\]
方程(17)在\(y\)方向上的微分形式为：
(19)\[
\frac{\p p}{\p y}=\sigma\kappa\frac{\p\alpha}{\p y}
\]
若考虑任意方向，在界面处方程(17)可以写为：
(20)\[
\nabla p=\sigma \kappa\nabla\alpha
\]
方程(20)表示在任意位置、任意方向上表面张力与压力降相平衡。
VOF方程
方程(20)的右侧即为动量方程的表面张力项。方程(1)还需要做进一步的变化，以使得边界条件的定义更加简单（在双流体模型中也可以进行类似的数学操作）。
注意：
interFoam求解器当中仅仅需要方程(20)。也就是说方程(20)之前的内容只是为了推导出方程(20)作铺垫。
首先定义
(21)\[
p_\mathrm{rgh}=p-\rho \bfg \cdot\bfh
\]
其中\(\bfh\)表示网格单元体心的位置矢量。对方程(21)进行梯度操作：
(22)\[
\nabla p_\mathrm{rgh}=\nabla p-\bfg\cdot \bfh \nabla \rho - \rho \bfg
\]
将其代入到方程(1)有：
(23)\[
\frac{\partial \rho \mathbf{U}}{\partial t}+\nabla \cdot (\rho \mathbf{U} \mathbf{U} ) - \nabla \cdot \boldsymbol{\tau} =-\nabla p_\mathrm{rgh}-\bfg\cdot \bfh \nabla \rho+\sigma \kappa \nabla \alpha
\]
其中的\(\boldsymbol{\tau}\)需要进一步模化，考虑牛顿流体：
(24)\[
\nabla\cdot\boldsymbol{\tau}=\nabla\cdot\left(\nu\left(\nabla\bfU+\nabla\bfU^{\mathbf{T}}\right)\right)
\]
其中粘度为
(25)\[
\nu = \alpha_1 \nu_1 + (1-\alpha_1)\nu_2
\]
即粘度为随着空间位置变化的量，其并非一个定值。因此，方程(24)可以简化为：
(26)\[
\nabla\cdot\boldsymbol{\tau}=\nabla\cdot\left(\nu\left(\nabla\bfU+\nabla\bfU^{\mathbf{T}}\right)\right)=\nabla\cdot\left(\nu\nabla\bfU\right)+\nabla\bfU\cdot\nabla\nu
\]
将其代入到方程(23)有VOF模型的动量方程：
(27)\[
\frac{\partial \rho \mathbf{U}}{\partial t}+\nabla \cdot (\rho \mathbf{U} \mathbf{U} ) - \nabla\cdot\left(\nu\nabla\bfU\right)-\nabla\bfU\cdot\nabla\nu =-\nabla p_\mathrm{rgh}-\bfg\cdot \bfh \nabla \rho+\sigma \kappa \nabla \alpha
\]
下面来推导VOF中的相方程。方程(1)中的密度\(\rho\)可以表示为：
(28)\[
\rho = \alpha_1 \rho_1 + (1-\alpha_1)\rho_2
\]
即：
(29)\[
\frac{\mathrm{D}\rho}{\mathrm{D}t} = \frac{\mathrm{D} \left(\alpha\left(\rho_1 - \rho_2 \right)+\rho_2 \right)}{\mathrm{D}t}= \frac{\mathrm{D}\alpha}{\mathrm{D}t}=\frac{\partial \alpha}{\partial t}+\bfU\cdot\nabla\alpha=0
\]
方程(29)即为不可压缩VOF模型中的相方程。综合考虑，不可压缩VOF模型中的方程为：
(30)\[
\frac{\partial \alpha}{\partial t}+\bfU\cdot\nabla\alpha=0
\]
(31)\[
\frac{\partial \rho \mathbf{U}}{\partial t}+\nabla \cdot (\rho \mathbf{U} \mathbf{U} ) - \nabla\cdot\left(\nu\nabla\bfU\right)-\nabla\bfU\cdot\nabla\nu =-\nabla p_\mathrm{rgh}-\bfg\cdot \bfh \nabla \rho+\sigma \kappa \nabla \alpha
\]
(32)\[
\nabla\cdot\bfU=0
\]
可见，VOF方程与单相流方程并无本质区别，均包含一个动量方程、一个连续型方程。其中连续性方程完全一致。动量方程，VOF模型中附加了随空间变化的粘度，以及附加表面张力项。在宏观流动中，附加的表面张力项\(\sigma \kappa \nabla \alpha\)可以忽略。
界面压缩
除此之外，包含了一个相传输方程，其可以看做是一个标量传输方程。但最重要的是，这里的标量传输，容不得半点的假扩散，否则会引起严重的数值问题。考虑网格非常细密的情况下，相分数应该只存在两个数值：0或者1。这种非常致密的网格会导致异常高的计算资源需求，因此VOF模型中不可避免的会存在\(\alpha\)在\(0-1\)之间的情况。但VOF应尽可能的使相界面足够的尖锐。在动网格算法中，界面的尖锐可以依附于网格的变化。在Front-tracking方法中，界面尖锐可以通过示踪颗粒来获得。历史上存在不同的可用于VOF模型中保证界面尖锐的方法。在OpenFOAM中采用的是Weller提出的方法，其通过一种人工的对流项来对相界面附近的相分数进行挤压来抗衡这种数值耗散带来的相界面模糊性，并且这一人工对流项在数值上需要保证非相界面处为零。依据添加人工对流项的思想，VOF模型可以表示为
(33)\[
\frac{\partial \alpha}{\partial t}+\nabla\cdot\left(\alpha\bfU\right)+\nabla\cdot\left(\alpha(1-\alpha)\bfU_c\right)=\alpha\nabla\cdot\bfU
\]
方程(33)中的第三项为人工添加的可压缩项，其在纯相（非界面处）计算域为\(0\)。仅仅在\(0 \leqslant\alpha\leqslant 1\)处存在值。\(\bfU_c\)为需要模化的速度。其应该在界面的法向上进行压缩而不是切向，否则引起虚假的扩散。因此\(\bfU_c\)的方向应与\(\bfn\)同向。因此有
(34)\[
\bfU_c=f\left(\frac{\nabla\alpha}{|\nabla\alpha|}\right)
\]
另一个问题是压缩速度的大小问题。很明显压缩速度不能过分大，这并不符合物理。因此压缩速度最大值也只不过是\(\bfU\)，则有：
(35)\[
\bfU_c=c|\bfU|\frac{\nabla\alpha}{|\nabla\alpha|}
\]
其中的\(c\)表示可控的压缩因子。当\(c=0\)，无压缩效果。\(c\)越大，压缩效应越快也越明显。最终有相方程：
(36)\[
\frac{\partial \alpha}{\partial t}+\nabla\cdot\left(\alpha\bfU\right)+\nabla\cdot\left(\alpha(1-\alpha)c|\bfU|\frac{\nabla\alpha}{|\nabla\alpha|}\right)=\alpha\nabla\cdot\bfU
\]
离散化与MULES
VOF模型的速度方程、连续性方程的离散化与单相流大同小异。详细的步骤可参考CFD:不可压瞬态PISO算法。在这里对其做简述。首先对方程(31)，省略方程右侧的项，进行有限体积离散有：
(37)\[
{A_\mathrm{P}}\mathbf{U}_\mathrm{P}^r{\rm{ + }}\sum {A_\mathrm{N}\mathbf{U}_\mathrm{N}^r} = S_\mathrm{P}^n
\]
求解后有预测速度\(\mathbf{U}_\mathrm{P}^r\)。预测速度并不符合连续性方程，考虑最终收敛的情况，对连续性方程进行离散有：
(38)\[
\sum \left(\mathbf{U}_{\mathrm{P},f}^{n+1} \cdot \bfS_f\right)=0
\]
如果能用压力表示方程(38)中的\(\mathbf{U}_{\mathrm{P},f}^{n+1}\)，则压力泊松方程即可构建。首先，收敛情况下方程(37)可以写为
(39)\[
{A_\mathrm{P}}\mathbf{U}_\mathrm{P}^{n+1}{\rm{ + }}\sum {A_\mathrm{N}\mathbf{U}_\mathrm{N}^{n+1}} = S_\mathrm{P}^n
-\nabla p_{\mathrm{rgh},\rP}-\bfg\cdot \bfh \nabla \rho_\rP+\sigma \kappa \nabla \alpha_\rP
\]
定义
(40)\[
\mathbf{HbyA}^{n+1}_\mathrm{P} = \frac{1}{{{A_\mathrm{P}}}}\left( { - \sum {{A_\mathrm{N}}\mathbf{U}_\mathrm{N}^{n+1}} + S_\mathrm{P}^n} \right)
\]
有
(41)\[
\mathbf{U}_\mathrm{P}^{n+1} = \mathbf{HbyA}^{n+1}_\mathrm{P}
-\frac{1}{A_\rP}\left(\nabla p_{\mathrm{rgh},\rP}^{n+1}+\bfg\cdot \bfh \nabla \rho_\rP^{n+1}-\sigma \kappa \nabla \alpha_\rP^{n+1}\right)
\]
依据Rhie-Chow插值，面上的速度为
(42)\[
\mathbf{U}_\mathrm{P,f}^{n+1} = \bfHbyA_{\rP,f}^{n+1}
-\frac{1}{A_{\rP,f}}\left(\nabla_f^\bot p_{\mathrm{rgh},\rP}^{n+1}+\bfg\cdot \bfh \nabla_f^\bot \rho_\rP^{n+1}-\sigma \kappa \nabla_f^\bot \alpha_\rP^{n+1}\right)
\]
将方程(42)代入到(38)有
(43)\[
\sum\left( \bfHbyA_{\rP,f}^{n+1}+\frac{1}{A_{\rP,f}}\left(\sigma \kappa \nabla_f^\bot \alpha_\rP^{n+1}-\bfg\cdot \bfh \nabla_f^\bot \rho_\rP^{n+1} \right)\right)=\sum \frac{1}{A_{\rP,f}}\left(\nabla_f^\bot p_{\mathrm{rgh},\rP}^{n+1}\right)
\]
即
(44)\[
\nabla\cdot\left(\frac{1}{A}\nabla p_{\mathrm{rgh}}^{n+1}\right)=\nabla\cdot\left(\bfHbyA^{n+1}+\frac{1}{A}\left(\sigma \kappa \nabla \alpha^{n+1}-\bfg\cdot \bfh \nabla\rho^{n+1}\right)\right)
\]
求解方程(44)既有收敛的压力。另外，interFoam中最重要的代码为\(\alpha\)方程的求解。在求解过程中，为了保证\(\alpha\)方程的严格有界。interFoam调用了FCT算法。在OpenFOAM中，FCT算法被称之为MULES。由于篇幅所限，在这里，MULES算法不会被详细的讨论，感兴趣的读者可以参考OpenFOAM中的MULES一节。
关键代码
interFoam中的速度方程通过下面的代码组建：
solve
(
UEqn
==
fvc::reconstruct
(
(
mixture.surfaceTensionForce()
- ghf*fvc::snGrad(rho)
- fvc::snGrad(p_rgh)
) * mesh.magSf()
)
);
其中的mixture.surfaceTensionForce()表示网格面上的表面张力，ghf*fvc::snGrad(rho)表示定义在网格面上的浮力项，顺气而然的，fvc::sngrad(p_rgh)表示定义在网格单元面上的压力项。这三项对应于方程(42)右边括号内的三项。之所以将这些力定义在面上，是为了消除可能的振荡的分布。