版本对应：

不管是OpenFOAM-11，还是老版本的OpenFOAM，势流求解器都是potentialFoam。

CFD: 势流算法

大量的流体力学现象，如尾涡和边界层现象，都和有旋流动密不可分。但无旋流同样大量的存在于某些细分的流体力学领域（如航空、地下水）。下图为一个圆柱势流场。很明显其是无旋的。对于无旋流的模拟，并不需要求解复杂的NS方程，求解势流方程即可，且势流方程是一个非常简单的拉普拉斯方程，求解起来非常快速。因此求解势流，可以用于快速的预估一个场来加速NS方程的迭代收敛。在势流求解算法中的主要问题是，因为速度势并不是原始变量，因此直接给速度势的边界条件在一般条件下是很困难的。因此势流求解算法，主要是研究如何通常通过速度边界条件，来隐性的施加到速度势边界条件。

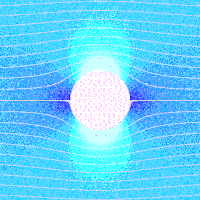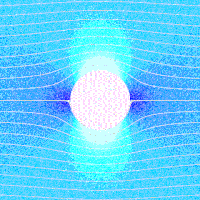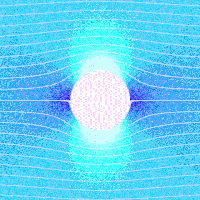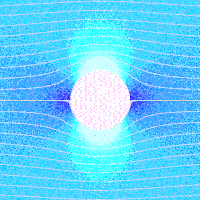
_images/potential.gif

普适性势流方程与求解

首先有稳态不可压缩流体连续性方程：

(1)\[ \nabla \cdot \bfU =0 \]

对于无旋流（\(\nabla\times\bfU=0\)），则必定存在一个势函数\(\Phi\)，使得

(2)\[ \nabla \Phi=\bfU \]

为了使得速度势与压力同向，在求解的时候同样也可以定义：

(3)\[ -\nabla \Phi=\bfU \]

本文选用方程(3)作为速度势的定义。

Warning

一维情况下方程(3)可以写为\(u=-\frac{\rd \Phi}{\rd x}\)。可见，如果\(x\)方向\(\Phi\)越大，则\(-\frac{\rd \Phi}{\rd x}=u\)为一个负数，其表示流体向\(x\)左侧移动，在这种情况下，\(\Phi\)的作用与压力作用相同。

对于不可压缩流动，将方程(3)代入到方程(1)，有：

(4)\[ -\nabla\cdot(\nabla \Phi)=0 \]

方程(4)即为控制势流的速度势方程。可以看出在不可压缩的情况下，速度势为一个拉普拉斯方程。给定\(\Phi\)的边界条件，就可以进行求解。

求解思想

从数学的角度来看，如果单独考虑方程(4)这个拉普拉斯PDE的话，或许可以通过下列边界条件求解：

  1. 进口\(\Phi\)固定值，出口\(\Phi\)固定梯度；

  2. 出口\(\Phi\)固定值，进口\(\Phi\)固定梯度；

  3. 进口、出口\(\Phi\)均给固定值；

  4. 给定方程(4)中的进出口固定梯度边界条件，同时给定任意网格的\(\Phi\)的值；

在CFD计算中，给定进口速度固定值是常规的处理方法。因此给定进口\(\Phi\)的固定梯度边界条件，是符合常理的。那么上述边界条件剩下2种：

  1. 第一种边界条件： 进口固定梯度；出口固定值；

  2. 第二种边界条件： 进口固定梯度；出口固定梯度；同时给定任意网格的\(\Phi\)的值；

下面我们来看上面2种中的哪一个更容易实施。考虑最简单的情况，仅仅有\(x\)方向，进出口速度必然是已知的（因为要满足通量守恒）。因此进出口的\(\Phi\)都可以给固定梯度边界条件，如\(\frac{\p\Phi}{\p x}\)在进出口都等于\(A\)。因此其可以用方程描述：

(5)\[ -\frac{\p}{\p x}\left(\frac{\p\Phi}{\p x}\right)=0, \frac{\p\Phi}{\p x}_{inlet}=\frac{\p\Phi}{\p x}_{outlet}=A \]

方程(5)是一个进出口固定梯度的边界条件组合，其由于相容性问题存在无穷多个解。在实际操作过程中，可以任意的固定某个网格点的\(\Phi\)值，方程(5)可以求出。参考\(\Phi\)值的不同，方程(5)的解不同，但\(\Phi\)的梯度相同，因此\(\bfU\)相同。因此在1D的情况，选用第2种边界条件进行求解非常合理。

Warning

方程(4)表示的是\(\nabla\Phi\)是一个固定的值，如果是1D情况，表示\(\Phi\)是一条直线。因此进出口的\(\frac{\p\Phi}{\p x}\)是相同的值。

对于3D的情况，能否选用第二种边界条件？

(6)\[ \nabla\Phi_{inlet}=\nabla\Phi_{outlet}=?A \]

这是不可以的。这是因为在3D的情况下，出口的速度一般呈现一种非均匀的分布，比如靠近壁面比较小，靠近管道中心比较大。因此\(\nabla\Phi_{outlet}=A\)是不成立的。因此出口的\(\Phi\)固定梯度边界条件不能给出。

那么能否使用第一种边界条件？答案是可以的。在这种情况下，如要证明第一种边界条件以及第二种边界条件在数值上相等。首先，两种边界条件进口都是固定梯度。因此不需要做对比。问题在于出口的固定值边界条件，是否等于固定梯度边界条件附加任意网格的\(\Phi\)值给定。

在进口速度给定的条件下，出口\(\Phi\)其实存在一个固定的梯度值，这个值虽然不能提前预先的知道，但为了满足质量守恒，\(\nabla\Phi\)一定是一个固定的数值。其取决于进口的速度（进口\(\Phi\)的固定梯度值以及网格）。因此，进口\(\Phi\)的固定梯度值以及网格，确定下来了\(\Phi\)曲面的形状。给定参考的\(\Phi\)的值，则是固定了\(\Phi\)的上下浮动空间。

举例，在1D情况下，考虑5个网格，\(\Phi\)可能的分布有2种：

1 2 3 4 5
10 11 12 13 14

上面5点连成的\(\Phi\)直线的斜率取决于进口速度，出口的\(\Phi\)的斜率也不能随意更改，比如要符合连续性方程，在这里就是与进口的斜率相同。任意网格的\(\Phi\)值固定之后，则固定了\(\Phi\)具体是那一条线。比如第一个网格的\(\Phi\)固定为1，那么\(\Phi\)的分布为：

1 2 3 4 5

比如第一个网格的\(\Phi\)固定为30，那么\(\Phi\)的分布为：

30 31 32 33 34

其都不影响速度的值。在这种情况下，如果固定出口的\(\Phi\)值，同样的，固定进口的斜率，也即第一种边界条件，则不需要给定参考网格的\(\Phi\)值。直接进行求解即可。比如出口的\(\Phi\)值固定为10，则有\(\Phi\)的分布为：

6 7 8 9 10

因此第一种边界条件，可以获得与第二种边界条件同样的结果，且不需要给定参考网格的\(\Phi\)值。第一种边界条件的数学描述可以表示为：

(7)\[ \nabla\Phi_{inlet}= u^{inlet}, \Phi_{outlet}=\mathrm{fixedValue} \]

其中的\(\nabla\Phi_{inlet}= u^{inlet}\)并结合计算域的形状，决定了\(\Phi\)曲面（假若为2D的情况）的分布。出口的\(\Phi_{outlet}=\mathrm{fixedValue}\)确定了\(\Phi\)的绝对范围。

OpenFOAM势流求解方法

因此，势流的求解边界条件，可以采用\(\Phi\)进口固定梯度，\(\Phi\)出口固定值的方法来实现。在OpenFOAM，其对其继续进行简化，将方程(7)做的更加普适性，使得进口可以采用零法向梯度来进行。其实二者的差异很小。只不过后者对用户更加友好（可以将\(\Phi\)的边界条件硬植入，不需要用户修改）。

_images/pt2.JPG

首先，给定上述的网格系统。现对方程(4)在进口边界处进行离散，其中调用固定梯度边界条件：

(8)\[ -\left( \frac{ \frac{\p\Phi}{\p x}_B-\frac{\p\Phi}{\p x}_A }{\Delta x} \right) =0 \]
(9)\[ -\left( \frac{\Phi_2-\Phi_1}{\Delta x} -\frac{\p\Phi}{\p x}_A \right) =0 \]
(10)\[ -\left( \frac{\Phi_2-\Phi_1}{\Delta x} \right) =\frac{\p\Phi}{\p x}_A=u_{inlet} \]

下面我们来看如何将其处理成零法向梯度边界条件，且获得同样的结果。

如果要通过零梯度边界条件来进行，即为\(\frac{\p\Phi}{\p x}_A=0\)。在这种情况下，方程(10)可以理解为\(\Phi\)在A处 ：

  1. 施加零梯度边界条件；

  2. 第1个网格点存在一个离散源项，其值为\(u_{inlet}\)；

Warning

同时要注意，这个源项仅仅在零法向梯度边界存在值。否则其与方程(7)不一致。

因此，可以将求解方程写为：

(11)\[\begin{split} &-\frac{\p}{\p x}\left(\frac{\p\Phi}{\p x}\right)=S_{cell} \\\\ &\frac{\p\Phi}{\p x}_{inlet}= 0, \Phi_{outlet}=\mathrm{fixedValue} \\\\ &S_{cell}=[u_{inlet},0,0,0,0,...,0]^T \end{split}\]

方程(11)与进口固定梯度边界条件，出口固定值边界条件是相等的。现在将其进行3维拓展。将方程(11)改写为：

(12)\[\begin{split} &-\nabla\cdot(\nabla \Phi)=S_{cell} \\\\ &\bfn\cdot\nabla\Phi_{inlet}=0, \Phi_{outlet}=\mathrm{fixedValue} \end{split}\]

方程(12)是OpenFOAM中植入的势流算法。最后一步是，如何把\(\bfU_{inlet}\)与源相\(S_{cell}\)建立关系。

非均一源项\(S_{cell}\)

首先，将\(-\nabla\cdot(\nabla\Phi)=0\)写成离散形式：

(13)\[ -\sum (\nabla\Phi)_f\cdot\bfS_f=0 \]

考虑进口边界相邻的这一个网格，其存在内部面，也存在边界进口面，因此其也可以写成：

(14)\[ -\sum (\nabla\Phi)_{内部面}\cdot\bfS_{内部面} -\sum (\nabla\Phi)_{进口}\cdot\bfS_{进口} =0 \]

在给定\((\nabla\Phi)_{进口}\)为固定值边界条件的时候，其等同于

(15)\[ -\sum (\nabla\Phi)_{内部面}\cdot\bfS_{内部面} -\sum \bfU_{进口}\cdot\bfS_{进口} =0 \]

移项有：

(16)\[ -\sum (\nabla\Phi)_{内部面}\cdot\bfS_{内部面} =\sum \bfU_{进口}\cdot\bfS_{进口} \]

方程(16)是针对边界处的网格（因为其存在内部面与边界进口面）。如果不对内部面以及边界面做区分，所有网格点的离散都可以写为：

(17)\[\begin{split} &-\sum (\nabla\Phi)_f\cdot\bfS_f=\sum \bfU_f\cdot\bfS_f, \\\\ &(\nabla\Phi)_{进口}=零法向梯度, \bfU_f^{边界}=固定值, \bfU_f^{内部}=0 \end{split}\]

注意，方程(17)中\(\bfU\)只有在进口边界处存在值，其内部场的值为0。因此，每一个网格上的源相\(S_{cell}\)就是：

(18)\[ S_{cell}=\sum \bfU_f\cdot\bfS_f \]

方程(17)写成连续形式即为：

(19)\[ -\nabla\cdot(\nabla \Phi)=\nabla\cdot\bfU, (\nabla\Phi)_{进口}=零法向梯度, \bfU_{内部}=0,\bfU_{进口}=固定值 \]

方程(19)为OpenFOAM最终植入的方程。

速度更新

在有了\(\Phi\)场之后，可以通过方程(3)，也即\(\bfU=-\nabla \Phi\)来计算速度。但是通过\(\bfU=-\nabla \Phi\)来计算速度，然后再从速度插值到通量这是不能满足通量守恒的。这种方法不会满足任何特性。仅仅是满足\(\bfU=-\nabla \Phi\)。

在方程(17)中，除了进口网格单元，其他网格点的源项\(S_{cell}=0\)。如果把\(-\nabla \Phi\)当做速度，会发现其表示\(-(\nabla \Phi)_f\)的通量是守恒的。因此重组\(-(\nabla \Phi)_f\)可以获得守恒的速度场。

考虑边界网格单元，\(-\sum (\nabla\Phi)_f\cdot\bfS_f=\sum \bfU_f\cdot\bfS_f\neq 0\)。但会发现

(20)\[ \sum (\bfU -\nabla\Phi )_f\cdot\bfS_f=0 \]

因此重组进口边界网格的\(-(\bfU -\nabla\Phi )_f\)可以获得守恒的速度场。其也可以认为变成了进口固定梯度边界条件。

代码分析

针对方程(19)中的\(\bfU_{内部}=0,\bfU_{进口}=固定值\)，通过下述代码进行：

volVectorField U
(
    IOobject
    (
        "U",
        runTime.timeName(),
        mesh,
        IOobject::MUST_READ,
        IOobject::AUTO_WRITE
    ),
    mesh
);

U = dimensionedVector(U.dimensions(), Zero);

方程(19)中的\(-\nabla\cdot(\nabla \Phi)=\nabla\cdot\bfU\)，通过下述代码进行：

fvScalarMatrix PhiEqn
(
    fvm::laplacian(dimensionedScalar(dimless, 1), Phi)
  ==
    fvc::div(phi)
);

方程(19)中的\((\nabla\Phi)_{进口}=零法向梯度\)，通过压力边界条件来进行（不需要显性的指定\(\Phi\)的边界条件）。例如在算例中，压力p还是通过常规的进口零法向梯度，出口固定值边界条件来设置。代码直接将压力的边界转移到\(\Phi\)边界。

下面的代码计算守恒的通量，以及重组速度场：

phi -= PhiEqn.flux();
U = fvc::reconstruct(phi);
U.correctBoundaryConditions();

下面的代码用来判断连续性方程误差：

Info<< "Continuity error = "
    << mag(fvc::div(phi))().weightedAverage(mesh.V()).value()
    << endl;

下面的代码，用来判断从守恒的通量场，重组后获得的速度场，继续插值到面上获得的通量场，与原本守恒通量场的误差：

Info<< "Interpolated velocity error = "
    << (sqrt(sum(sqr(fvc::flux(U) - phi)))/sum(mesh.magSf())).value()
    << endl;