用户指南:第1章
后向台阶流为一个二维的、等温的、不可压缩流动。其计算域特征如下:
左边存在一个进口(v=10 m/s);
右边存在一个出口(P=0 Pa);
上下均为壁面边界;
在OpenFOAM-11中,将调用incompressibleFluid模块。
前处理
OpenFOAM所有自带的算例都存储在$FOAM_TUTORIALS文件夹中。需要首先将相应的算例,复制到一个文件夹下。在本算例中,我们将自带算例复制到$FOAM_RUN文件夹下。用户需要分3步运行下述代码:
cd $FOAM_RUN
cp -r $FOAM_TUTORIALS/incompressibleFluid/pitzDailySteady .
cd pitzDailySteady
在输入第一行代码“cd $FOAM_RUN”的时候,如果输出:
dyfluid@dyfluid-virtual-machine:~$ cd $FOAM_RUN
bash: cd: /home/dyfluid/OpenFOAM/dyfluid-11/run: No such file or directory
则需要手动创立一个文件夹:
cd /home/dyfluid/OpenFOAM
mkdir dyfluid-11
cd dyfluid-11
mkdir run
注意:
上方代码中的“dyfluid”为您的用户名。如果您的ubuntu系统的用户名为“pangmao”,则需要把相应的“dyfluid”改为“pangmao”。
然后执行
cd $FOAM_RUN
cp -r $FOAM_TUTORIALS/incompressibleFluid/pitzDailySteady .
cd pitzDailySteady
输入如下命令,可打开当前文件夹,即可看到pitzDailySteady文件下的3个子文件夹。所有OpenFOAM算例文件夹主要分为3个:0文件夹、constant文件夹和system文件夹。在0文件夹里,可以设置算例的初始条件。在constant文件夹里,可以设置算例的物理性质。在system文件夹,主要设置算例的算法控制。该算例文件夹下还存在一个Allrun文件,其主要用于自动处理脚本。
nautilus .
网格生成
OpenFOAM使用blockMesh来生成网格。blockMesh在生成网格的时候需要指定特别复杂的点位置信息。因此,blockMesh只能用于生成一些简单模型的网格。当然了,blockMesh可以生成复杂模型的网格,但是需要花费大量的时间来写点位置信息。OpenFOAM中的blockMesh主要是结合snappyHexMesh来划分网格。snappyHexMesh为OpenFOAM内置的另外一个网格生成程序,将会在后文介绍。本算例采用blockMesh来生成一个简单的网格。
blockMesh的字典文件在system文件夹下,字典内容如下所示。
1/*--------------------------------*- C++ -*----------------------------------*\
2 ========= |
3 \\ / F ield | OpenFOAM: The Open Source CFD Toolbox
4 \\ / O peration | Website: https://openfoam.org
5 \\ / A nd | Version: dev
6 \\/ M anipulation |
7\*---------------------------------------------------------------------------*/
8FoamFile
9{
10 format ascii;
11 class dictionary;
12 object blockMeshDict;
13}
14// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
15
16// Note: this file is a Copy of $FOAM_TUTORIALS/resources/blockMesh/pitzDaily
17
18convertToMeters 0.001;
19
20vertices
21(
22 (-20.6 0 -0.5)
23 (-20.6 25.4 -0.5)
24 (0 -25.4 -0.5)
25 (0 0 -0.5)
26 (0 25.4 -0.5)
27 (206 -25.4 -0.5)
28 (206 0 -0.5)
29 (206 25.4 -0.5)
30 (290 -16.6 -0.5)
31 (290 0 -0.5)
32 (290 16.6 -0.5)
33
34 (-20.6 0 0.5)
35 (-20.6 25.4 0.5)
36 (0 -25.4 0.5)
37 (0 0 0.5)
38 (0 25.4 0.5)
39 (206 -25.4 0.5)
40 (206 0 0.5)
41 (206 25.4 0.5)
42 (290 -16.6 0.5)
43 (290 0 0.5)
44 (290 16.6 0.5)
45);
46
47negY
48(
49 (2 4 1)
50 (1 3 0.3)
51);
52
53posY
54(
55 (1 4 2)
56 (2 3 4)
57 (2 4 0.25)
58);
59
60posYR
61(
62 (2 1 1)
63 (1 1 0.25)
64);
65
66
67blocks
68(
69 hex (0 3 4 1 11 14 15 12)
70 (18 30 1)
71 simpleGrading (0.5 $posY 1)
72
73 hex (2 5 6 3 13 16 17 14)
74 (180 27 1)
75 edgeGrading (4 4 4 4 $negY 1 1 $negY 1 1 1 1)
76
77 hex (3 6 7 4 14 17 18 15)
78 (180 30 1)
79 edgeGrading (4 4 4 4 $posY $posYR $posYR $posY 1 1 1 1)
80
81 hex (5 8 9 6 16 19 20 17)
82 (25 27 1)
83 simpleGrading (2.5 1 1)
84
85 hex (6 9 10 7 17 20 21 18)
86 (25 30 1)
87 simpleGrading (2.5 $posYR 1)
88);
89
90boundary
91(
92 inlet
93 {
94 type patch;
95 faces
96 (
97 (0 1 12 11)
98 );
99 }
100 outlet
101 {
102 type patch;
103 faces
104 (
105 (8 9 20 19)
106 (9 10 21 20)
107 );
108 }
109 upperWall
110 {
111 type wall;
112 faces
113 (
114 (1 4 15 12)
115 (4 7 18 15)
116 (7 10 21 18)
117 );
118 }
119 lowerWall
120 {
121 type wall;
122 faces
123 (
124 (0 3 14 11)
125 (3 2 13 14)
126 (2 5 16 13)
127 (5 8 19 16)
128 );
129 }
130 frontAndBack
131 {
132 type empty;
133 faces
134 (
135 (0 3 4 1)
136 (2 5 6 3)
137 (3 6 7 4)
138 (5 8 9 6)
139 (6 9 10 7)
140 (11 14 15 12)
141 (13 16 17 14)
142 (14 17 18 15)
143 (16 19 20 17)
144 (17 20 21 18)
145 );
146 }
147);
148
149// ************************************************************************* //
如上图所示,在blockMeshDict字典文件中,第22行至第44行的坐标值,为图中编号从0至21的位置点坐标信息。convertToMeters关键词用于尺寸缩放。例如,当为1时,则所有数字的单位均为米;当为10时,则所有数值需要乘以10(单位为米)。
由上图可知,计算域分解成了5个block,因此在blockMeshDict中的blocks关键词下存在5个block的设置。blockMeshDict文件的内容将在此进行简要介绍,详细信息请参阅后文章节(待更新)。
该blockMeshDict文件定义了5个block,每个bock由3组代码定义。第1组:以hex关键词开头,表示每个block都是六面体形状,hex关键词后面列出了8个顶点的标签。第2组:每个block的各个方向上的单元数量,由3个整数组成的向量来指定。例如,第一个block指定了(18 30 1),表明在x方向划分出18个单元格,在y方向划分30个单元,在z方向(未启用的方向)上仅划分1个单元格。
这些block的网格是非均匀划分的,后文会详细阐述。
定义对应面网格为入口、出口和壁面等边界,具体包含以下几个部分:upperWall和lowerWall代表壁面;inlet和outlet分别代表进、出口。z方向上的边界归入一个名为frontAndBack的区域中。由于本算例为一个2D模型,因此frontAndBack是一个empty的边界条件类型。
具体来说,通过在blockMeshDict文件上运行blockMesh来生成网格。在本案例中,需要在终端输入如下内容:
blockMesh
执行命令后,在终端窗口中可查看blockMesh的运行状态。如果blockMeshDict文件中有任何错误,blockMesh会输出相应的错误提示。
查看网格
在计算之前需要先检查网格,可通过在终端执行paraFoam命令启动ParaView查看网格。
所有linux程序均可通过如下两种方式运行:
前端运行:即终端会等待该程序执行完毕后才结束;
后端运行:在运行的同时,可以执行其他程序。
如果希望运行ParaView时,同步运行其它程序,可执行如下命令实现:
paraFoam &
然后在“Properties”窗口的“Mesh Parts”面板中选择要查看的几何图形,点击“Apply”。如果网格的边界数量比较少,可以选中“Mesh Parts”面板上面的复选框快速选择所有边界。完成选择后可点击“Apply”。

点击ParaView顶部的第二行图标可以设置网格的不同显示形式,也可以通过下面的Display面板来进行设置,操作如下:
选择Solid Color确定颜色;
点击Edit按钮(位于“着色”部分内),选择一个合适的颜色,比如黑色;
在Representation菜单中选择Wireframe模式,这样网格显示更加清晰;背景颜色可以在 Properties窗口底部的 View(Render View)面板中进行设置;
另外,属性窗口中的很多高级设置,需要通过点击窗口顶部搜索框旁边的“高级属性”(图标“⚙️”)才能显示出来。
边界和初始条件
网格划分完成后,可以设置初始场。该案例为非稳态流动,求解时间从t = 0s开始,因此初始场数据被存储在cavity文件夹的0文件夹中。这个0文件夹包含几个文件,其中包括压力p和速度U,首先查看p文件:
16dimensions [0 2 -2 0 0 0 0];
17
18internalField uniform 0;
19
20boundaryField
21{
22 inlet
23 {
24 type zeroGradient;
25 }
26
27 outlet
28 {
29 type zeroGradient;
30 value uniform 0;
31 }
32
33 upperWall
34 {
35 type zeroGradient;
36 }
37
38 lowerWall
39 {
40 type zeroGradient;
41 }
42
43 frontAndBack
44 {
45 type empty;
46 }
47}
该文件主要有三个关键词:
dimensions 单位:这里是运动压力,即\(\mathrm{m}^2 \mathrm{s}^{-2}\)(即压力与密度之比);
internalField 内部场的值:其可以是均一值,也可以是非均一值。若内部场为非均一值,则必须为所有网格指定具体值;
boundaryField 边界场的值:包括边界条件和所有边界块的数据;
对于pitzDailySteady案例,初始场是均一值。
Note
由于是不可压缩流动,压力类型是运动压力,且压力绝对值并不重要,因此为方便起见,将其设置为uniform 0。
边界包括upperWall, lowerWall, inlet和outlet。壁面和入口的压力p边界类型均为zeroGradient,表示压力的法向梯度为零。出口使用了给定值fixedValue边界条件,压力值设为uniform 0。二维模拟的两侧平面的frontAndBack边界面指定为empty。
速度U的初始值设为0,通过3个分量来表示,即(0 0 0)。在壁面上应用无滑移条件noSlip。入口流速U在x方向大小为10m/s,通过fixedValue条件进行设置,数值为uniform (10 0 0)。出口使用zeroGradient,frontAndBack面设为empty。
物性
物性参数设置均在constant目录下的字典文件中,在physicalProperties文件中指定物性参数:
17viscosityModel constant;
18
19nu 1e-05;
其中的viscosityModel设置粘度nu为常数。nu关键词来指定运动粘度大小,运动粘度用希腊符号\(\nu\)表示,大小为1e-05。
湍流模型
为了确定流动是否为湍流,需要估算雷诺数。雷诺数的定义为:
\(\bfU\)和\(L\)分别代表特征速度和特征长度,\(\nu\)表示运动粘度。本算例入口台阶高度\(L =25.4\)mm,当速度大小为10m/s时,雷诺数\(Re=25400\)。对于管内流动,当雷诺数\(Re > 2000\)时,流动状态通常会由层流转捩为湍流,所以该算例为湍流。
momentumTransport文件中可以设置牛顿流体、非牛顿流体、湍流以及粘弹性等。本算例中部分湍流模型设置如下:
17simulationType RAS;
18
19RAS
20{
21 // Tested with kEpsilon, realizableKE, kOmega, kOmega2006, kOmegaSST, v2f,
22 // ShihQuadraticKE, LienCubicKE.
23 model kEpsilon;
24
25 turbulence on;
26
27 printCoeffs on;
28
29 viscosityModel Newtonian;
30}
simulationType需指定层流或湍流,RAS表示雷诺平均湍流模型。RAS子字典中包含一个model关键词,该关键词若为kEpsilon,则表示其为\(k-\varepsilon\)模型。turbulence关键字如果是on,表示开启湍流模型。所有湍流模型都有默认值,这些默认值可以在momentumTransport文件中通过指定关键词来进行设置。当打开printCoeffs时,到终端将会显示系数。
Note
viscosityModel关键词表示流体为牛顿流体,流体类型默认为牛顿流体的时候其可以省略。
\(k-\varepsilon\)模型需要求解包含湍流动能\(k\)和湍流耗散率\(\varepsilon\)的输运方程。在0文件夹下的k和epsilon文件中,对湍流动能\(k\)和湍流耗散率\(\varepsilon\)的初始化和边界条件分别进行设置。
湍流变量的边界场要尽可能准确,以使计算容易收敛。湍流动能\(k\)可以通过以下公式计算:
其中,\(I\)表示湍流强度。在本例中估算\(I=0.05\),故 \(k=1.5\times \left ( 10\times 0.05 \right ) ^{2}=0.375 \rm m^{2} \rm s^{-2}\)。因此,在k文件中0.375可以同时用以初始内部场和入口值。
湍流耗散率 \(\varepsilon\) 可计算为:
湍流耗散率 \(\varepsilon\) 可以通过 \(C_{\mu}=0.09\) 和普朗特混合长度 \(l_{\rm m} \) 的估值来计算。在本算例中,\(l_{m}\)为台阶高度的0.1倍,即2.54mm, 从而得到\(\varepsilon =0.09^{0.75} \times 0.375^{1.5} /0.00254=14.855 \rm m^{2} \rm s^{-3} \)。在epsilon文件中,14.855同时用作初始内部场和入口值。
Note
\(l_{m}\)与\(I\)是需要自行预估的变量。
在模拟壁面的时候,可使用壁面函数。壁面函数通过0文件夹下的nut、k以及epsilon文件来指定。首先查看nut文件:
16
17dimensions [0 2 -1 0 0 0 0];
18
19internalField uniform 0;
20
21boundaryField
22{
23 inlet
24 {
25 type calculated;
26 value uniform 0;
27 }
28 outlet
29 {
30 type calculated;
31 value uniform 0;
32 }
33 upperWall
34 {
35 type nutkWallFunction;
36 value uniform 0;
37 }
38 lowerWall
39 {
40 type nutkWallFunction;
41 value uniform 0;
42 }
43 frontAndBack
44 {
45 type empty;
46 }
47}
本案例采用标准壁面函数,分别在upperWall和lowerWall通过nutkWallFunction类型进行指定。还可以选择其它壁面函数模型还包括,如通过nutRoughWallFunction关键字进行指定粗糙壁面函数。同时,epsilon相应的壁面需指定为epsilonWallFunction,k需要指定为kqRWallFunction。
Note
kqRWallFunction是一种通用的边界条件,可应用于任何湍流动能类型的场,例如\(k\)、\(q\) 或雷诺应力\(\bfR\)。
求解设置
controlDict文件可以对求解层面的进行相应设置。其位于system目录下:
16
17application foamRun;
18
19solver incompressibleFluid;
20
21startFrom startTime;
22
23startTime 0;
24
25stopAt endTime;
26
27endTime 2000;
28
29deltaT 1;
30
31writeControl timeStep;
32
33writeInterval 100;
34
35purgeWrite 0;
36
37writeFormat ascii;
38
39writePrecision 6;
40
41writeCompression off;
42
43timeFormat general;
44
45timePrecision 6;
46
47runTimeModifiable true;
48
49cacheTemporaryObjects
50(
51 kEpsilon:G
52);
53
54functions
55{
56 #includeFunc streamlinesLine
57 (
58 name=streamlines,
59 start=(-0.0205 0.001 0.00001),
60 end=(-0.0205 0.0251 0.00001),
61 nPoints=10,
62 fields=(p k U)
63 )
64
65 #includeFunc writeObjects(kEpsilon:G)
66}
关键词incompressibleFluid表示模拟不可压缩等温流体的稳态或瞬态流动,同时支持动网格。
本算例的模拟从t=0s时刻开始,因此求解器从0文件夹中读取数据。如此,需要将startFrom关键字设为startTime,并将startTime关键字设定为0。
本算例为稳态模拟,意味着所有方程中的时间导数 \(∂/∂t\) 均为0。可以在fvSchemes文件中,将ddtSchemes设置为steadyState来实现。在稳态情况下,因为不再用于离散化 \(∂/∂t\),所以关键字deltaT表示的时间步长仅用作时间增量。关键字deltaT的值不会影响计算结果,因此对于稳态模拟,deltaT值设置为1,仅仅表示代表求解步数。
endTime用于设置求解停止的时间,设为2000可以提供足够多的求解步数,使稳态解能够收敛。
当运行计算时,若希望在特定的时间间隔内记录结果,writeControl提供了多种选项来设定记录结果的时间点。这里的timeStep选项指定了每隔n个时间步记录一次结果,n的值由writeInterval关键字指定。如果间隔设为100,那么结果将在第100步、第200步等时间点被记录;OpenFOAM在每次写入一组数据时,都会创建一个以当前时间命名的新目录,例如100。新目录包含所有的场的信息。
数值离散和线性求解器
在system目录下的fvSchemes文件中,可对有限体积离散化方案进行设置。在system目录下的fvSolution文件中,可设置线性方程求解器、容差和其他算法控制的规格。
这两个文件的详细信息分别在4.5和4.6节中描述。对于这个算例,需要注意以下几点:
fvSchemes文件中的ddtSchemes 默认为stableState,以调用稳态计算;
稳态求解器使用基于SIMPLE的算法,在fvSolution文件中的SIMPLE子字典中设置其控制项;
SIMPLE子字典包含一个consistent开关,设置为yes,采用SIMPLE算法的“consistent”形式 (SIMPLEC);
SIMPLEC的收敛对fvSolution文件中的relaxationFactors非常敏感;经过测试,0.9的取值并不适合标准的SIMPLE算法;
SIMPLEC的收敛性较敏感,通常仅适用于几何形状简单的情况。
运行应用程序
在对单一区域进行模拟时,可采取foamRun应用。它从controlDict文件中的solver加载相关的求解器模块来执行计算。本案例中,通过在终端中输入以下内容来运行foamRun。
foamRun
在终端窗口可查看求解进度,包含连续的求解步骤,速度分量和压力值的初始和最终残差,以及连续性方程的误差。
fvSolution中的SIMPLE包括一个residualControl子字典,其中包含一组p、U和湍流场的容差。当所有场的残差低于其各自的容差时,incompressibleFluid求解器将终止计算。在此示例中,求解器在287次迭代后终止,并显示以下提示。
SIMPLE solution converged in 287 iterations
求解结果写入pitzDailySteady目录内的时间目录中,可使用“ls”命令列出目录内容,以查看包含结果的时间目录(100、200和287)。
ParaView中的时间选择
当结果写入时间目录,可通过命令paraFoam打开ParaView查看。第一步是激活时间选择器,设置顶部第一行按钮右侧的“Time”框以选择时间目录,如图7.4所示。
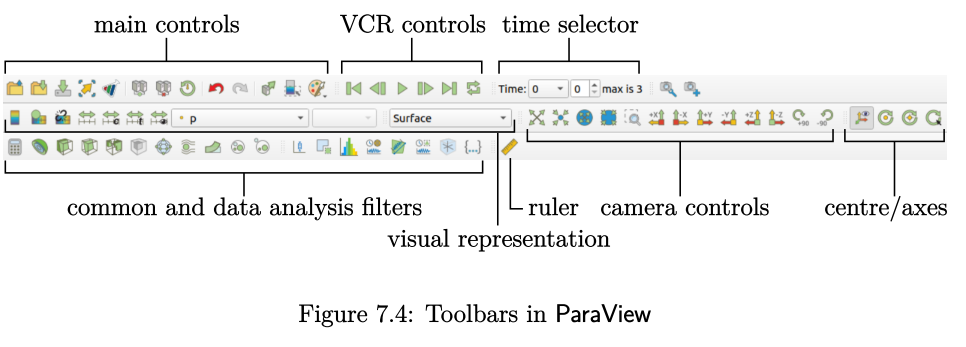
如果在没有生产任何时间目录(即只有一个0目录)前打开ParaView,则必须重新激活时间选择器,通过以下方式更新时间目录内容:
在ParaView 左下方界面,点击properties窗口的顶部(如有必要,向上滚动面板);
切换面板顶部的“缓存网格”(Cache Mesh)按钮(位于“刷新时间”(Refresh Times))按钮下方;
单击“Apply ”按钮。
随后,Time选择器更新,Time变成一个下拉菜单,其中包含案例中的时间目录(0、100、200和287)。若要查看时间步为287时的解,将当前时间步更改为287即可。
对于教程其余部分:
在ParaView中,如果窗口面板(例如“Properties”)没有想要的关键词,需确保在 Pipeline Browser 中突出显示相关模块(以蓝色显示)。例如,仅当选择顶部模块(此处为pitzDailySteady.OpenFOAM)时,“Refresh Times”才会出现。
云图
按照图2.4所示可生成压力云图,从ParaView顶部的第二行图标中进行选择,或者滚动到“Properties”中的“Display”面板,然后进行如下设置:
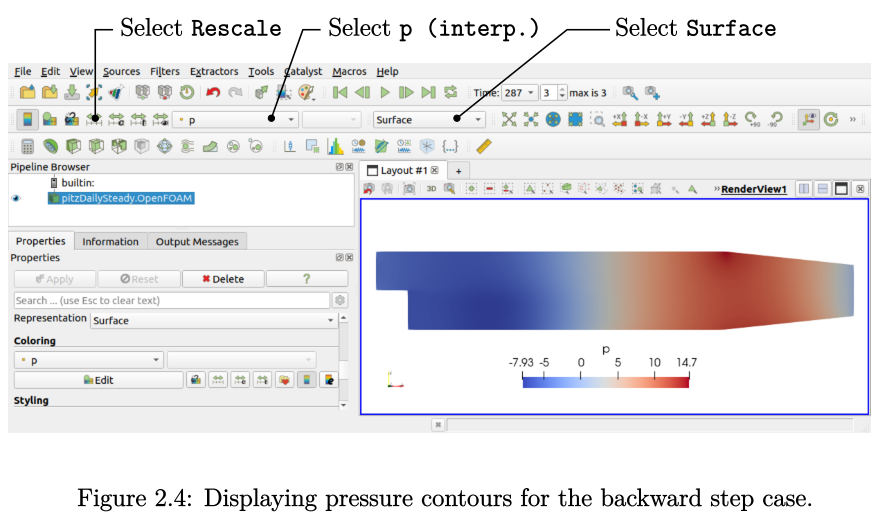
压力场如上图所示,在出口通道收缩时压力增加到最大值。使用点图标( ),压力场在每个单元之间进行插值,使压力场的颜色光滑过渡。相反,如果从“Coloring”菜单中选择单元格图标(
),压力场在每个单元之间进行插值,使压力场的颜色光滑过渡。相反,如果从“Coloring”菜单中选择单元格图标( ),则每个单元格将被赋予一个压力值,则压力场单元格由单一颜色表示。
),则每个单元格将被赋予一个压力值,则压力场单元格由单一颜色表示。
颜色图例可以通过点击ParaView顶部第二行按钮左侧的“Toggle Color Legend Visibility”按钮来切换显示或隐藏。这些按钮是“Active Variable Controls”工具栏的一部分,如图7.4所示。点击“Active Variable Controls”工具栏中左侧的第二个按钮“Edit Color Map”,可打开“Color Map Editor”窗口,如图2.5所示,可以在这设置颜色比例尺和颜色条等属性。
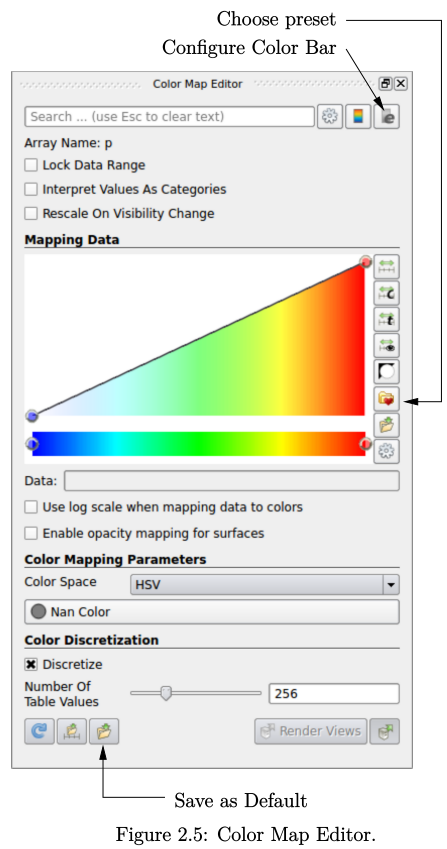
需要注意,ParaView默认使用蓝色-白色-红色的颜色比例尺,而不是更常见的蓝色-绿色-红色(彩虹)。因此,当第一次执行ParaView时,需要更改颜色比例尺。可以在“Color Scale Editor”中选择“Choose Preset”按钮(带有心形图标)来完成。CFD的常规颜色比例尺是“Blue to Red Rainbow”,仅当在搜索栏中输入名称或选中该栏右侧的齿轮图标时才会列出。
选择“Blue to Red Rainbow”并单击“Apply”和“Close”后,单击面板底部的“Save as Default”按钮(文件保存符号),以便ParaView默认采用这种类型的图例。
可通过单击搜索栏最右侧的“Edit Color Legend Properties”来设置颜色图例,例如设置文本大小、字体类型和缩放比例,如图 2.5 所示。
切面
在图像窗口中,按住鼠标左键并拖动鼠标可旋转图像,图像根据压力值大小对整个几何表面进行着色。若要生成二维等高线图,首先创建一个切面,即“slice”。在Pipeline Browser窗口中,pitzDailySteady.OpenFOAM模块后突出显示 。从ParaView顶部菜单的“Filters”菜单中可选择“Slice”。可以在“Common”子菜单中找到“Slice”,或者在ParaView顶部的第三行图标中找到“Common and Data Analysis”图标(见图7.4)。
选择“Slice”会在Pipeline Browser中创建一个新项。在“Properties”窗口中,单击Z法线按钮,切平面的原点应位于z轴上的某一点,例如(0,0,0),法线设置为(0,0,1)。
单击“Apply”后,在“RenderView”窗口中将出现切片,而原始的pitzDailySteady.OpenFOAM模块将消失。每个模块的显示和隐藏可以通过Pipeline Browser中每个模块左侧的圆点图标来启用和禁用。
需要注意:在ParaView中,如果RenderView窗口中没有显示关键词,通过打开Pipeline Browser中的圆点按钮来确保相关模块可见。
矢量图
在绘制流速矢量前,首先在Pipeline Browser中选中“Slice”模块,单击其左侧的圆点按钮来隐藏显示。为了在每个单元的中心生成一个速度矢量图,首先需要从网格几何体中过滤出单元中心,如7.1.7节所述。在Pipeline Browser中高亮显示pitzDailySteady.OpenFOAM模块后,从“Filters->Alphabetical”菜单中选择“cell centers”,然后单击“Apply”。
在Pipeline Browser中突出显示Centers后,从“Filters->Common”菜单(或第三行按钮)中选择“Glyph”,属性窗口面板如图 2.6 所示。
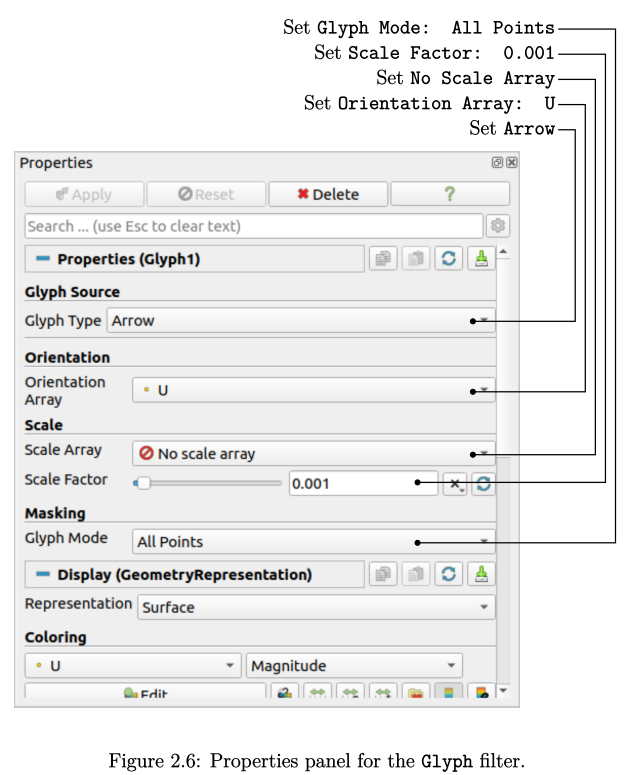
对于速度矢量图,glyphs设置如下4项:
Arrow,控制glyph类型;
Orientation Array,控制箭头方向;
Scale Array and Scale Factor,控制箭头长度;
Glyph Mode,控制箭头的数量。
单击“Apply”后,glyphs显示为单色,例如白色。 在“Coloring”下拉菜单中,可设置根据速度U大小给glyphs着色。
“Legend”设置。单击“Edit Color Map”(第2行左侧的第2个图标),随即打开“Color Map Editor ”窗口。单击搜索框右侧的“Advanced Properties”齿轮按钮搜索框,可打开“Edit Color Legend Properties”窗口。
标题和标签设置。对于图2.7,标题设置为“U[m/s]”。通过取消“Automatic Label Format”并在“Label Format”文本框中输入%-#6.1f,可以将标签指定为1位固定小数点。然后,取消选中“Add Range Labels”。
图2.7显示台阶下游部分再循环区域的局部放大图。在下壁面,glyphs指向与壁面附近流动相反的方向。上述情况是由于这些glyphs被绘制在壁面边界块的中心,并且为无滑移条件,速度大小为0而引起的。向量没有任何方向,ParaView将箭头定向为默认的x方向。快速删除这些向量的方法是:
返回到Pipeline Browser顶部的pitzDailySteady.OpenFOAM模块;
在“Properties”的Mesh Parts 面板中,取消选中 lowerWall patch;
点击 “Apply”。

常用组件
ParaView包含200多个组件,这些组件可以通过“Filters->Alphabetical”菜单查看。由于只有一小部分组件与CFD相关,因此建议将这些组件添加到“Filters->Favourites”菜单中。从“Filters->Favourites”菜单中选择“Manage Favourites”,搜索如下组件,然后单击“Add>>”添加到“Favourites”菜单中。
Extract Block,用于选择域的组件,例如边界块和内部单元;
Slice,用于在几何体中插入一个平面;
Cell Centers and Glyph, 主要用于绘制速度矢量图;
Stream Tracer and Tube, 用于绘制流线;
Contour,用于在表面上绘制等高线和等值面;
Feature Edges,用于捕捉表面上的特征以获得更好的图像清晰度。
等高线
在绘制流速的等高线前,先在“Pipeline Browser”中选择“Glyph”模块,并点击其左侧的圆点图标以隐藏该模块。随后,选中“Slice”模块,并按流速U来着色。然后在切面上以U数列(1、2、…、10)来绘制等高线。
对切片应用“Contour”组件。此组件能够依据标量的恒定值,在二维空间中绘制线条或在三维空间中绘制曲面。由于U是一个向量,因此不能直接根据U绘制等高线。为此,需要生成一个表示U大小的标量场。
使用函数对象进行后处理来生成mag(U)场,具体方法在7.3节中有详细描述。首先运行foamPostProcess工具,可通过以下方式使用“-func”选项来调用mag函数对象:
foamPostProcess -func "mag(U)"
该程序会逐个处理所有时间目录, 并读取每个时间目录内的U值,计算其大小“mag(U)”。然后将结果作为字段文件存回相应的时间目录。接下来,需要将mag(U)字段加载到ParaView中,操作步骤如下:1. 在“Pipeline Browser”中找到pitzDailySteady.OpenFOAM,点击“Refresh Times”;2. 滚动至“Fields”面板,选中mag(U)后点击“Apply”。
在“Pipeline Browser”中再次选中“Slice”模块,并应用“Contour”过滤器。3. 在“Properties”面板中,从“Contour By”下拉菜单里选择mag(U)。4. 在“Isosurfaces”部分,先点击“-”按钮清除默认值,然后按照图2.8所示添加10个值。5. 可以选择以Wireframe形式展示等高线,并使用纯黑色进行着色。
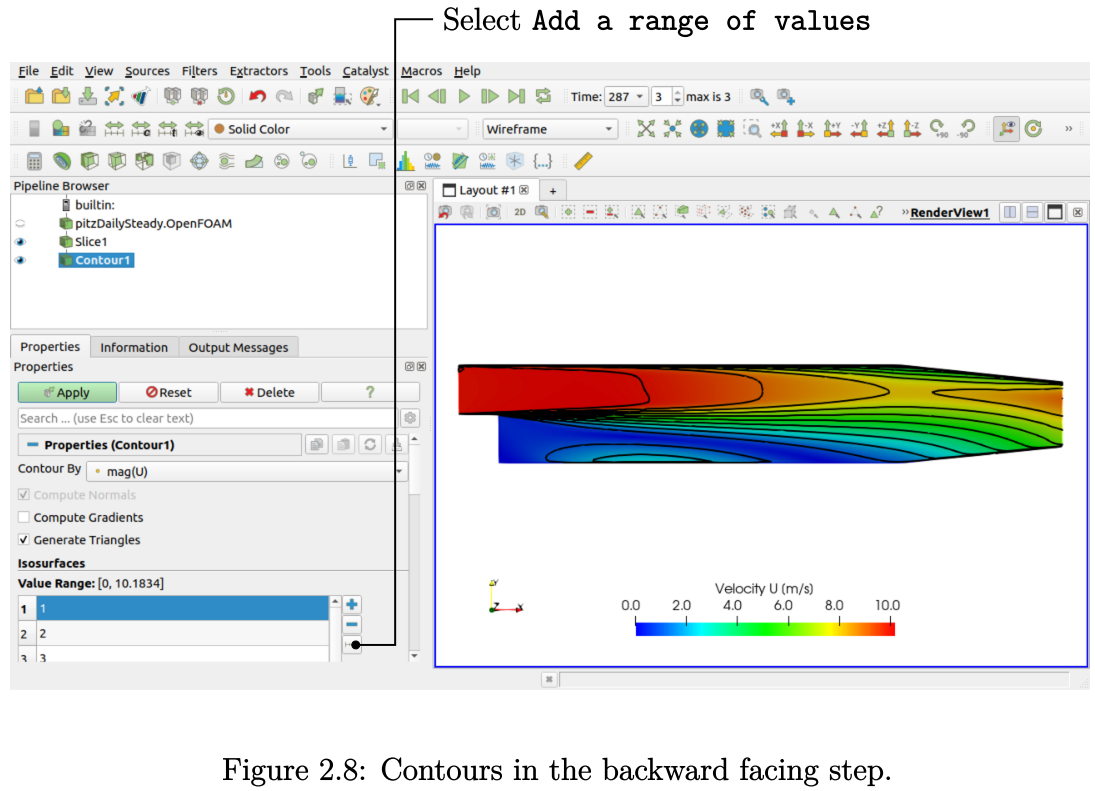
流线图
在绘制流线之前,首先隐藏“Contour”模块,然后在“Pipeline Browser”中选择“Slice”模块,随后选中“Stream Tracer”组件。
可以看到打开了一个新的“StreamTracer”模块,可通过“Properties”窗口进行设置。在流场中每一点上都与速度矢量相切的曲线称为流线。若选择“Integration Direction BOTH”,则流线线条会在“Seeds”的上游和下游都进行绘制。滚动“Properties”窗口来设置 “Seeds”,默认的Seed Type为“Line”,即沿着在指定点之间绘制的“Seeds”。在“Line Parameters”中,将两点设置为从(0, −0.025, 0)到(0.2, 0.025, 0)。分辨率则指定了沿线条分布的“Seeds”数量,建议减少到25个。点击“Apply”后,将生成如图2.9所示的追踪器,并可通过调整线条点和分辨率来获得不同的流线结果。
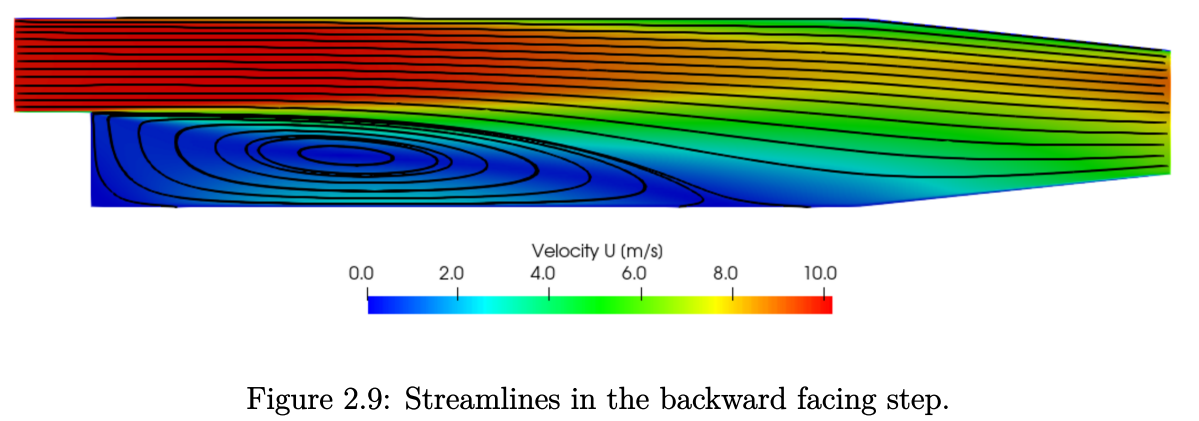
入口边界条件
检查流动域的入口边界处的流动状况是必要的。在\(0/U\)中,将速度条件设定为固定值(10 0 0),且这个速度值应用于入口边界的所有面。入口与无滑移条件的墙壁边界相邻,这会导致相邻边界面之间的流速发生突变。
先用鼠标右键放大到几何图形的入口区域。随后,在“Pipeline Browser”中激活“Slice”模块,并根据p值的cell values来着色(选择  )。为了突出显示入口附近单元格的压力变化,可根据图2.10所示,设定一个自定义范围,即 \(-5 < p < -1\)。若要自定义范围,可点击“Rescale to Custom Data Range”按钮(
)。为了突出显示入口附近单元格的压力变化,可根据图2.10所示,设定一个自定义范围,即 \(-5 < p < -1\)。若要自定义范围,可点击“Rescale to Custom Data Range”按钮( , 该按钮位于第2行图标中,从左数第5个)。之后会弹出一个面板,在此输入范围的最小值和最大值,再点击“Rescale”按钮。若要查看速度分布图,需返回“Pipeline Browser”中的“Glyph”模块,并将其设置为可见。根据流速调整箭头大小,可以绘制出相应的图像。在“Glyph”的Properties中,滚动到“Scale”面板,将“Scale Array”设置为U,选择“Scale By Magnitude”并设定一个Scale Factor为8e-05。最后,设置Solid Color为白色。
, 该按钮位于第2行图标中,从左数第5个)。之后会弹出一个面板,在此输入范围的最小值和最大值,再点击“Rescale”按钮。若要查看速度分布图,需返回“Pipeline Browser”中的“Glyph”模块,并将其设置为可见。根据流速调整箭头大小,可以绘制出相应的图像。在“Glyph”的Properties中,滚动到“Scale”面板,将“Scale Array”设置为U,选择“Scale By Magnitude”并设定一个Scale Factor为8e-05。最后,设置Solid Color为白色。
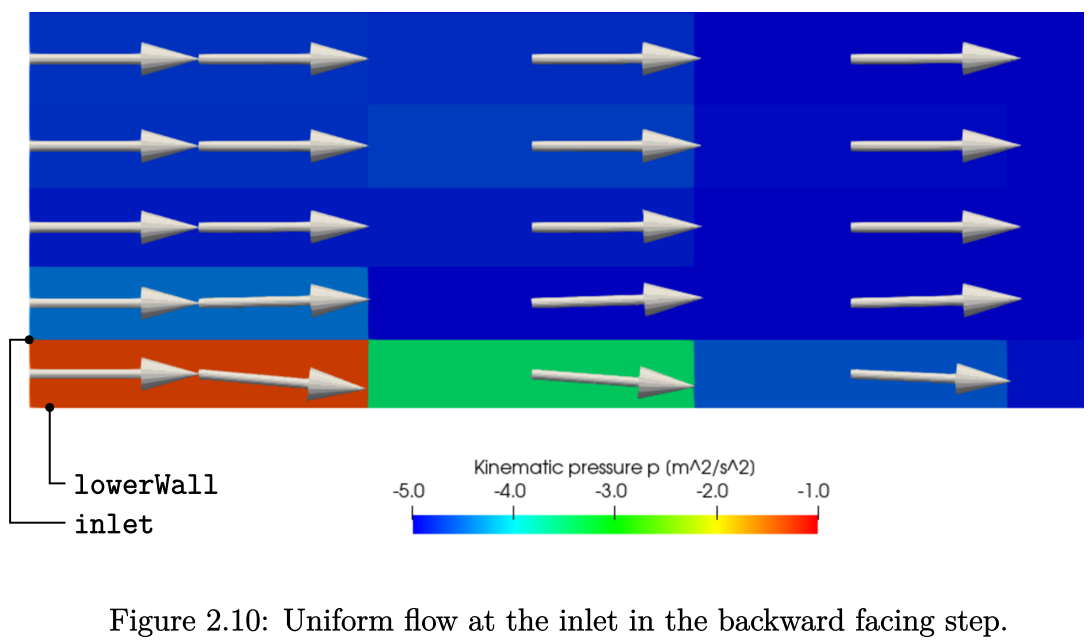
图示为入口区域与下侧壁边界的相邻部分。在图左侧所示,速度矢量均匀分布。由于壁面上的剪切力作用,流动在近壁处减小。这种减速会引起压力增加,从而产生一个驱动力梯度,使流动略微偏离壁面,以保证质量守恒。
为了减小入口壁面附近压力的增加,通过调整边界条件,使得入口速度不再保持均一。其中,“flowRateInletVelocity”边界条件是用于指定入口流量的通用U边界条件。可以使用“foamInfo”脚本来查看这一边界条件的详细文档。这个脚本是一个通用工具,能够提供OpenFOAM中应用程序、模型和工具的文档。对于“flowRateInletVelocity”边界条件,可以按以下方式运行该脚本(请注意,有时为了简化,该名称可以缩写,比如这里使用“flowRateInlet”而非“flowRateInletVelocity”)。
foamInfo flowRateInlet
foamInfo脚本能够定位并输出相关代码的头文件,并从中提取“Description”和“Usage”。此外,它还能识别出相关的模型(在这种情况下指的是其他边界条件),并列出使用该模型的示例案例。虽然foamInfo脚本并非尽善尽美,但在大多数情况下,能迅速提供有用的信息。
根据文档内容,入口速度条件可通过massFlowRate, volumetricFlowRate 或 meanVelocity 来指定流量。在文本编辑器中打开“\(0/U\)”文件,找到入口区域的边界字段关键词。随后,可以通过设置inlet子字典来应用meanVelocity条件,设置方式如下:
inlet
{
type flowRateInletVelocity; // modify
meanVelocity 10; // insert
value uniform (10 0 0); // leave
}
此条件会对边界上的速度进行评估,并为边界区域上的所有面设定相应的值。尽管对于OpenFOAM而言,“值”这一关键词是多余的,但ParaView需要它来显示初始化区域字段的初始值。因此,保留了“值”关键词,以便于ParaView的使用。
保存“\(0/U\)”文件之后,可以重新求解。首先确认“flowRateInletVelocity”是否成功模拟原始的“fixedValue”条件。在“controlDict”文件中,案例的起始时间设定为0,并且它将覆盖时间文件夹中的先前结果。只需重新运行“foamRun”求解器,即可测试新的条件。
foamRun
求解器的运行过程与之前相同,最终在287次迭代后结束。打开ParaView,并在“Pipeline Browser”的“pitzDailySteady.OpenFOAM”模块中点击“Refresh Times”按钮。结果未发生变化,这表明“flowRateInletVelocity”在此阶段设置了一个统一的值“(10 0 0)”。
通过包含速度的profile文件来修改\(0/U\)”文件中的“flowRateInletVelocity” 条件。 文档中强调了两个自定义的分布函数:turbulentBL和laminarBL,它们分别为充分发展的湍流和层流边界层提供power-law和quadtratic。在此案例中,按以下方式将turbulentBL分布添加到边界条件中:
inlet
{
type flowRateInletVelocity;
meanVelocity 10;
profile turbulentBL; // add
value uniform (10 0 0);
}
在重新运行模拟之前,建议先删除先前的求解结果时间文件夹,以避免混淆。因为求解器可能会在不同的时间点终止计算,如果不删除先前的结果,旧案例的最终时间文件夹中的结果将不会被新结果覆盖,这可能会导致错误。
foamListTimes实用工具为用户提供了一种快速简便的方式来删除求解结果的时间文件夹,同时保留“0”文件夹。首先,终端中按如下方式运行foamListTimes:
foamListTimes
执行上述命令后,会返回求解结果时间文件夹的列表,其中包括100、200和287,但不包括“0”文件夹。要删除这些的文件夹,可以在foamListTimes命令中添加“-rm”删除选项,即运行以下命令:
foamListTimes -rm
删除包含先前结果的时间文件夹,接下来运行foamRun求解器。此时,foamRun在277次迭代后终止。然后,返回ParaView,并在“Pipeline Browser”的“pitzDailySteady.OpenFOAM”模块中点击“Refresh Times”按钮。
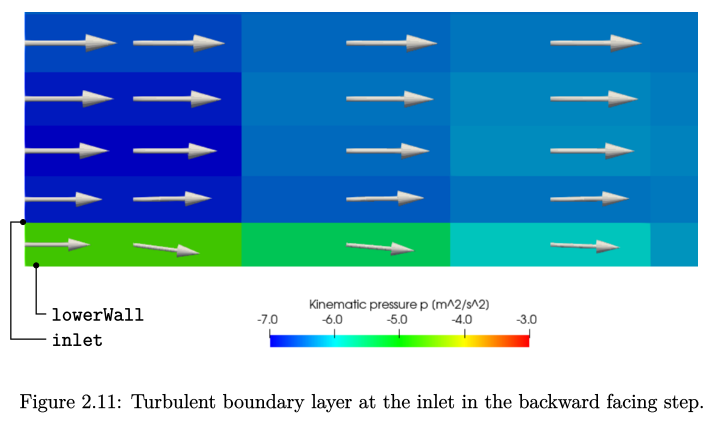
输出时间的变化可能会让ParaView造成混乱,导致它在时间选择器中显示带有“?”符号。为了解决这个问题,可以恢复到时间0,或者点击“Cache Mesh”和“Apply”来重建选择器关键词。然后,选择序列中的最后一个时间点(277)。此时,更新速度剖面和压力,如图2.11所示。对于压力,自定义范围调整为 \(-7<p<-3\)。入口处的速度不再保持均匀,而是根据turbulentBL函数形成了一个特定的剖面。与下壁面相邻面的速度与之前相比显著降低,因此近壁单元内由剪切力引起的减速效应也相应减弱。结果显示,左上角与其周围单元之间的压力差没有以前那么大,现在大约是 \(+2 \rm m^{2} s^{-2} \)(从-7变为-5),而之前则是 \(+4 \rm m^{2} s^{-2} \)(从-5变为-1)。
湍流模型
后向台阶案例的设计初衷是让大家能够快速尝试多种不同的湍流模型。在constant文件夹中的momentumTransport文件内,有一条注释详细列出了在此案例上测试过的各种湍流模型。部分模型除了求解k和ε的方程外,还求解如ω(omega)等其他场的方程。为了尽可能减少在更换模型时的工作量,在0文件夹中已经预先包含了这些其他场的相关文件。同样,在system文件夹中的fvSchemes和fvSolution文件里也分别加入了这些场的计算方案和求解器的相关关键词。
为了更改湍流模型,应在文本编辑器中打开momentumTransport文件。通过如下设置,将模型切换为realizable k - ε模型。
model realizableKE;
若要重新运行计算,需要先删除求解结果的时间文件夹,然后执行以下foamRun命令:
foamListTimes -rm
foamRun
求解器在进行了255次迭代后终止。返回ParaView,并点击“Refresh Times”按钮来查看第255秒的结果。结果如图2.12所示,该图使用了之前设置好的速度场切面和流线组件。
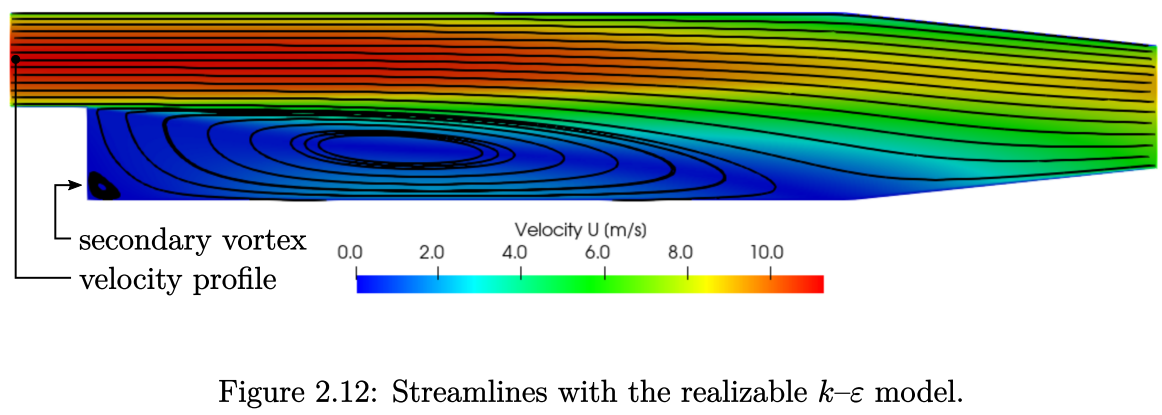
相比标准k - ε模型,realizable k - ε模型的扩散性更低。realizable k - ε模型能够捕捉到台阶底部的一个二次流涡,其高度大约是台阶高度的一半。此外,再循环区域也更长,再附着现象发生在下壁面,并且开始逐渐收窄直至出口的位置。
大家也可以尝试其它湍流模型。在工业CFD领域,k-ω SST模型备受欢迎,可以通过在momentumTransport文件中进行以下设置来选择该模型。
model kOmegaSST;
这个模型需要对湍流动能耗散率ω进行初始化。这个参数的计算方法与等式2.3中的ε类似,具体计算方式如下,其中会用到\(l_{m} \):
使用之前的估计 \(l_{m} =2.54\)mm,则 \(\omega =0.09^{-0.25} \times 0.375^{0.5} /0.00254=440.2\rm s^{-1} \)。 在 \(0/omega \)文件中,440.2 用于初始internalFields和入口value。
随后,删除求解结果的时间文件夹,执行foamRun命令,并使用此模型重新模拟。值得注意的是,这次求解器不会因为fvSolution文件的residualControl子字典中指定的残差控制容差范围内收敛而提前终止。相反,它会在达到2000次迭代时终止,这是controlDict文件中设定的 endTime。
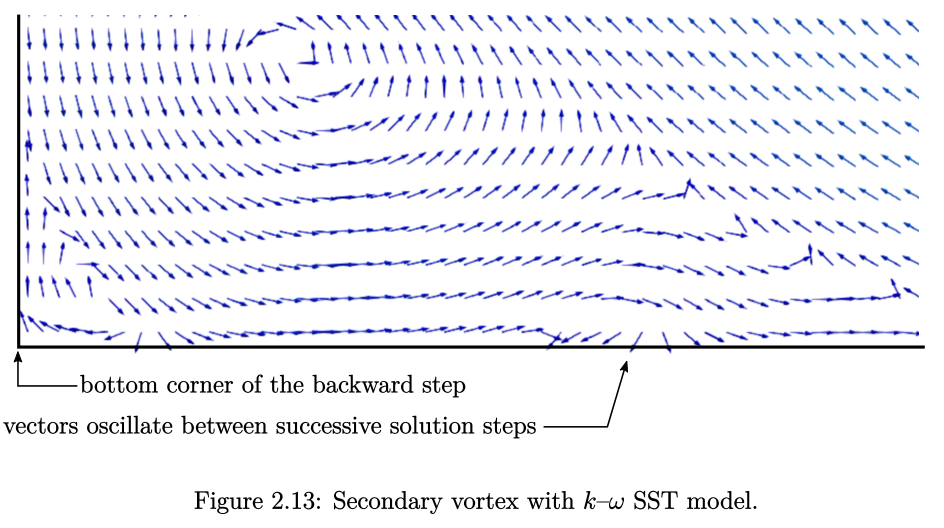
采用k-ω SST模型的结果显示,在台阶的底部存在一个更大的二次流涡。这个二次流涡并没有达到稳定状态,而是在连续的求解步骤中出现小幅度的振荡。这些振荡可以通过观察不同的求解步骤(如1000、1100、1200等)中的速度矢量来发现。图2.13展示了次级涡旋的范围,并指出了在二次流涡重新附着点周围矢量振荡的位置。
可以通过修改对流项的数值方法,以此来稳定二次流涡。应从“system”文件夹中打开“fvSchemes”文件。在“divSchemes”子字典中,通过形如“div(phi,…)”的关键词来指定对流项的离散化方式。目前对流项采用的是线性迎风格式,具体如下所示。
div(phi,U) bounded Gauss linearUpwind grad(U);
linearUpwind格式根据单元梯度,通过外推法将场从单元中心插值到单元面上。其中的grad(U)关键词用于确定梯度计算的方式,具体采用“gradSchemes”子字典中指定的方案。在本算例中,仅包含一个default格式,用于计算所有方程式中的所有梯度项。
gradSchemes
{
default Gauss linear;
grad(U) cellLimited Gauss linear 1;
}
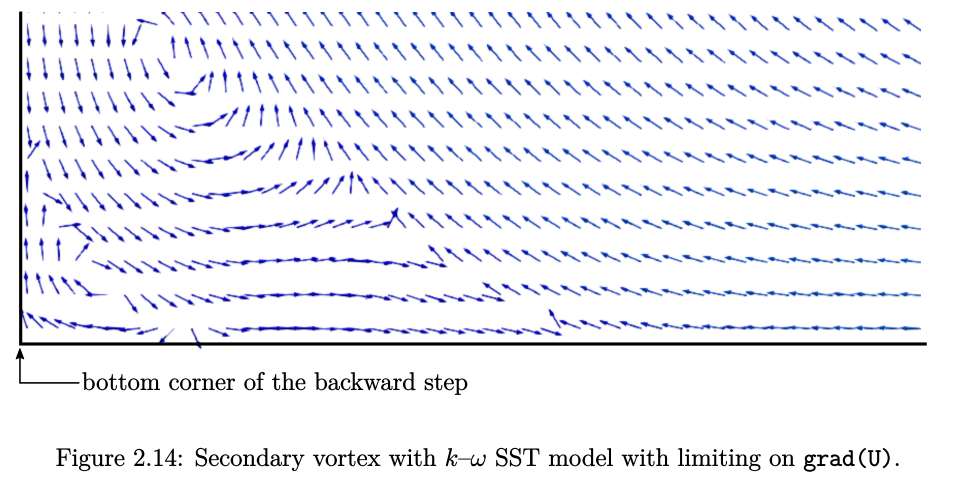
保存fvSchemes文件之后,可以删除先前的时间文件夹,执行foamRun命令来重新运行计算。应用cellLimited格式后,计算会正常收敛,求解器在迭代285次后终止。此时,二次流涡会稳定下来,如图2.14所示。