用户指南:第3章
本案例对正方形孔板进行线性弹性稳态应力分析,包含预处理、求解计算和后处理。如图2.20所示,正方形孔板的尺寸为:正方形板边长为L=4 m,孔半径R=0.5 m。板的左右两端面施加σ=10 kPa的均匀拉力。该模型上下、左右均对称,因此可将仿真几何模型简化为初始几何的1/4,如图中阴影区域所示。
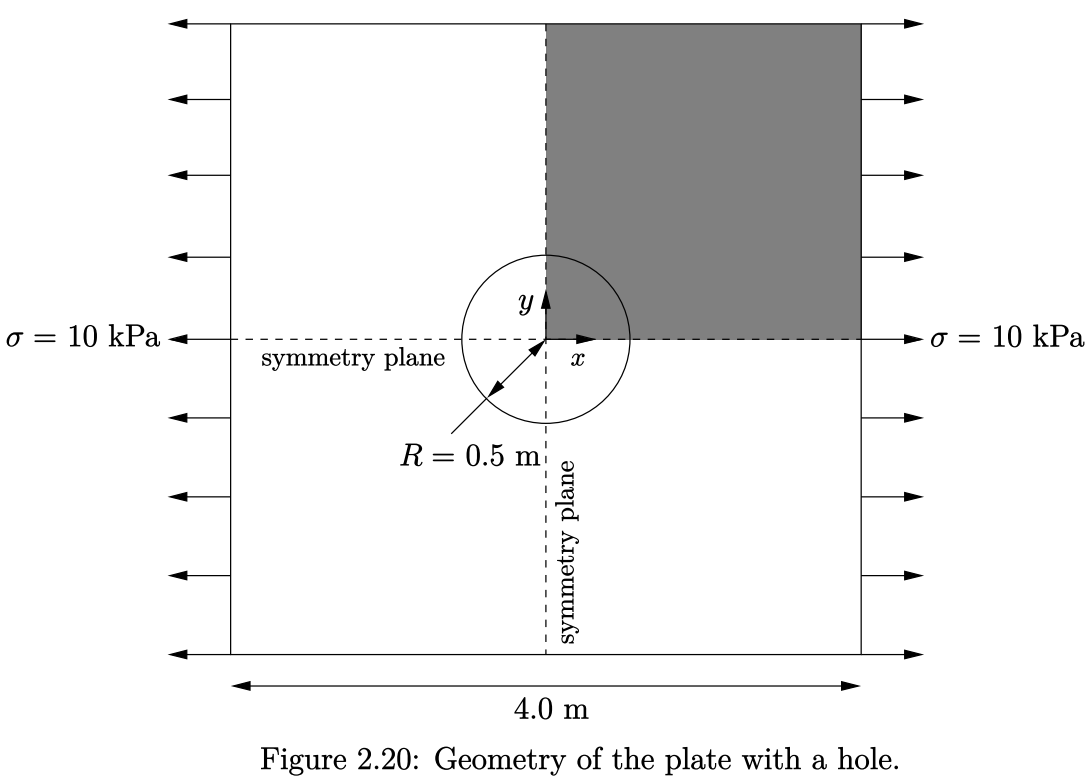
由于载荷是作用在平面上,所以该案例可近似看作二维模型。关于模型在厚度方向上的分析,有如下两个假设:(1)平面应力条件,即假定二维平面外的应力分量可以忽略不计;(2)平面应变条件,即假定二维平面外的应变分量可以忽略不计。对于此案例,平面应力条件适用于厚度较小的固体;而平面应变条件则适用于厚度较大的固体。
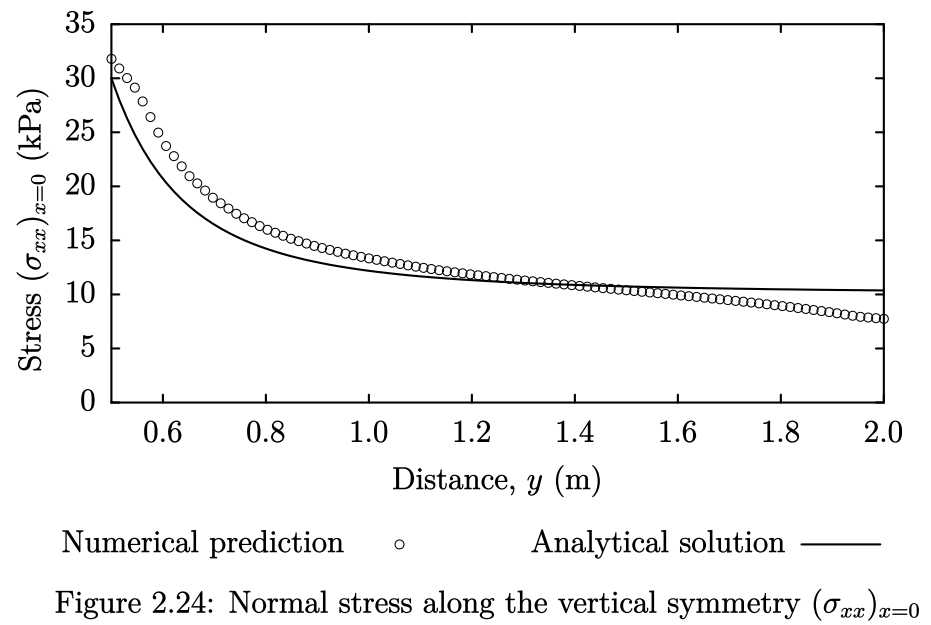
对于一个带有圆孔的无穷大薄板存在一个解析解。垂直于对称垂直平面正应力的解为
大家可自行将数值解与解析解进行对比分析,还可以研究网格分辨率和网格分级对数值解的影响。并且,可以增加板与孔的尺寸,然后对无限大平板的解析解,与有限尺寸平板的数值解,进行对比分析。
本案例使用了solidDisplacement模块化求解器。首先,进入run目录,从$FOAM_TUTORIALS/solidDisplacement目录中复制plateHole案例,然后进入到plateHole案例目录。
run
cp -r $FOAM_TUTORIALS/solidDisplacement/plateHole .
cd plateHole
网格生成
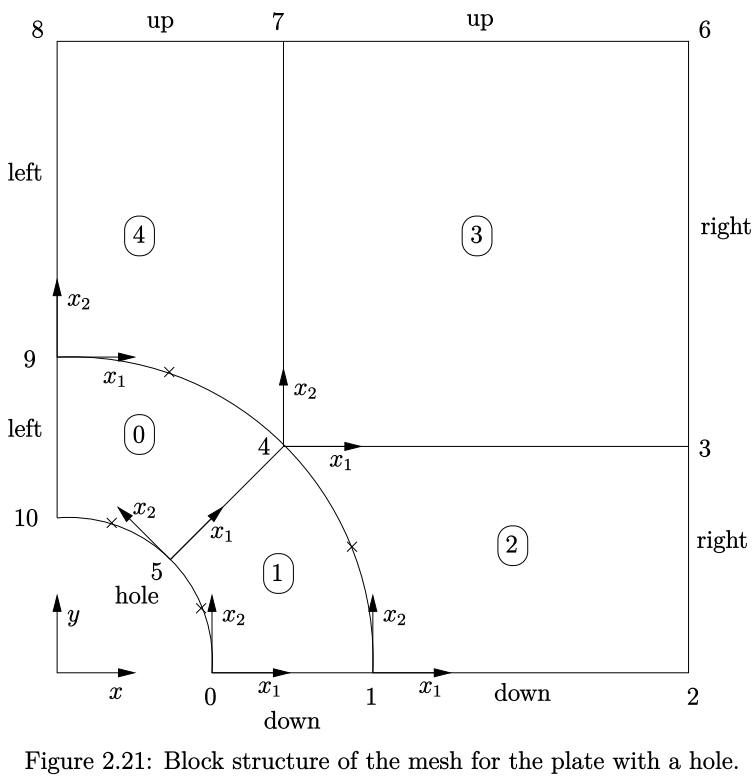
如图2.21所示为该案例的网格。网格由四个区域组成,其中一个区域具有弧形边界。如第2.1.2节中所述,即使在OpenFOAM中将案例视为二维模型,但所有的几何图形都是在三维空间中生成的。因此,需要设置z方向上的block尺寸,该案例设置为0.5m。由于牵引边界条件被指定为应力而非力,与横截面积无关。可在编辑器中打开blockMeshDict文件,如下所示。
16convertToMeters 1;
17
18vertices
19(
20 (0.5 0 0)
21 (1 0 0)
22 (2 0 0)
23 (2 0.707107 0)
24 (0.707107 0.707107 0)
25 (0.353553 0.353553 0)
26 (2 2 0)
27 (0.707107 2 0)
28 (0 2 0)
29 (0 1 0)
30 (0 0.5 0)
31 (0.5 0 0.5)
32 (1 0 0.5)
33 (2 0 0.5)
34 (2 0.707107 0.5)
35 (0.707107 0.707107 0.5)
36 (0.353553 0.353553 0.5)
37 (2 2 0.5)
38 (0.707107 2 0.5)
39 (0 2 0.5)
40 (0 1 0.5)
41 (0 0.5 0.5)
42);
43
44blocks
45(
46 hex (5 4 9 10 16 15 20 21) (10 10 1) simpleGrading (1 1 1)
47 hex (0 1 4 5 11 12 15 16) (10 10 1) simpleGrading (1 1 1)
48 hex (1 2 3 4 12 13 14 15) (20 10 1) simpleGrading (1 1 1)
49 hex (4 3 6 7 15 14 17 18) (20 20 1) simpleGrading (1 1 1)
50 hex (9 4 7 8 20 15 18 19) (10 20 1) simpleGrading (1 1 1)
51);
52
53edges
54(
55 arc 0 5 (0.469846 0.17101 0)
56 arc 5 10 (0.17101 0.469846 0)
57 arc 1 4 (0.939693 0.34202 0)
58 arc 4 9 (0.34202 0.939693 0)
59 arc 11 16 (0.469846 0.17101 0.5)
60 arc 16 21 (0.17101 0.469846 0.5)
61 arc 12 15 (0.939693 0.34202 0.5)
62 arc 15 20 (0.34202 0.939693 0.5)
63);
64
65boundary
66(
67 left
68 {
69 type symmetryPlane;
70 faces
71 (
72 (8 9 20 19)
73 (9 10 21 20)
74 );
75 };
76 right
77 {
78 type symmetryPlane;
79 faces
80 (
81 (2 3 14 13)
82 (3 6 17 14)
83 );
84 };
85 down
86 {
87 type symmetryPlane;
88 faces
89 (
90 (0 1 12 11)
91 (1 2 13 12)
92 );
93 }
94 up
95 {
96 type patch;
97 faces
98 (
99 (7 8 19 18)
100 (6 7 18 17)
101 );
102 }
103 hole
104 {
105 type patch;
106 faces
107 (
108 (10 5 16 21)
109 (5 0 11 16)
110 );
111 }
112 frontAndBack
113 {
114 type empty;
115 faces
116 (
117 (10 9 4 5)
118 (5 4 1 0)
119 (1 4 3 2)
120 (4 7 6 3)
121 (4 9 8 7)
122 (21 16 15 20)
123 (16 11 12 15)
124 (12 13 14 15)
125 (15 14 17 18)
126 (15 18 19 20)
127 );
128 }
129);
130
131
132// ************************************************************************* //
在之前案例中几何模型中仅包含直边,本案例几何模型包含曲边,在 edges 关键字条目下指定非直边列表。列表中的每个条目的书写格式以曲线的类型开始,包括 arc、simpleSpline、polyLine 等,详细描述见 5.4.3 节。在本案例中,曲边都是圆弧形的,因此可以通过 arc 关键字条目指定。后续条目是圆弧的起始顶点和结束顶点的标签,以及圆弧经过的点向量。
图2.21所示,blockMeshDict中,block的方向不一致。block 0的 \(x_2\) 方向与block 4的 \(-x_1\) 方向一致。这意味着需要谨慎定义每个block的单元格数量和分布,以便block相邻面上的单元格能够匹配。
定义了六个面:包含3个侧平面,1个圆弧面,1个正面和1个背面,其中左侧面和下侧面是对称平面。对称平面为场边界,需要在网格定义中进行设置。因此,左侧面和下侧面定义为的symmetryPlane类型,如blockMeshDict文件所示。
frontAndBack面代表在二维情况下,被忽略的平面。这同样是一个几何约束,因此在网格内部定义,使用blockMeshDict中显示的empty类型。有关边界类型和几何约束的详细信息,可参考第5.3节。
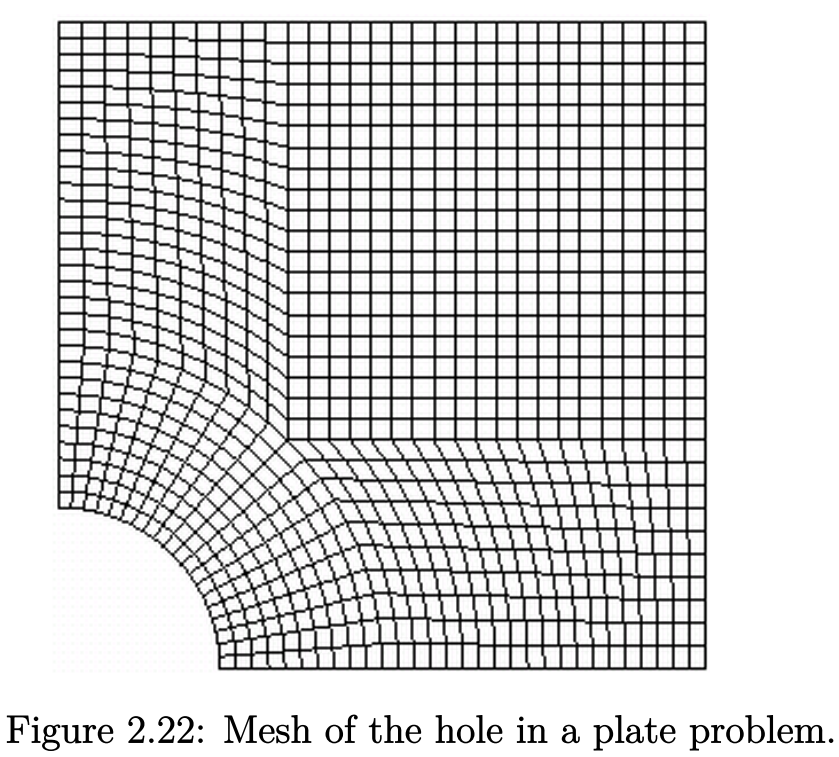
其余的面都是常规patch类型。可使用blockMesh生成网格,并按照第2.1.3节中的描述在paraFoam中查看,网格如图2.22所示。
边界和初始条件
网格生成完成后,需要设置包含边界条件的初始场。对于不考虑热效应的应力分析情况,只需要设置位移D。0文件夹中的D文件内容如下:
16dimensions [0 1 0 0 0 0 0];
17
18internalField uniform (0 0 0);
19
20boundaryField
21{
22 left
23 {
24 type symmetryPlane;
25 };
26 right
27 {
28 type tractionDisplacement;
29 traction uniform (10000 0 0);
30 pressure uniform 0;
31 value uniform (0 0 0);
32 }
33 down
34 {
35 type symmetryPlane;
36 }
37 up
38 {
39 type tractionDisplacement;
40 traction uniform (0 0 0);
41 pressure uniform 0;
42 value uniform (0 0 0);
43 }
44 hole
45 {
46 type tractionDisplacement;
47 traction uniform (0 0 0);
48 pressure uniform 0;
49 value uniform (0 0 0);
50 }
51 frontAndBack
52 {
53 type empty;
54 }
55}
56
57// ************************************************************************* //
首先,可以看到位移的初始条件设置为(0,0,0) m。左侧面和下侧面均为symmetryPlane类型,与constant/polyMesh/boundary文件网格描述中的设置一致。同理,frontAndBack面设置为empty。
其余面应用牵引边界条件,设置为tractionDisplacement边界类型。牵引边界条件需要指定两个变量:1)边界牵引矢量,其通过traction指定,2)牵引力大小,其通过关键词pressure来指定。因为up与hole边界是无牵引边界。因此pressure都是0。对于右侧面,牵引力应为(1e4, 0, 0)Pa,压力应为0 Pa。
物性
物性在constant目录中的physicalProperties字典中设置,如下所示:
16
17rho
18{
19 type uniform;
20 value 7854;
21}
22
23nu
24{
25 type uniform;
26 value 0.3;
27}
28
29E
30{
31 type uniform;
32 value 2e+11;
33}
34
35Cv
36{
37 type uniform;
38 value 434;
39}
40
41kappa
42{
43 type uniform;
44 value 60.5;
45}
46
47alphav
48{
49 type uniform;
50 value 1.1e-05;
51}
52
53planeStress yes;
54thermalStress no;
55
56
57// ************************************************************************* //
该文件包括钢的材料属性:
密度 \(\rm rho = 7854kg·m^{-3} \)
杨氏模量 \(\rm E=2\times 10^{11} Pa\)
泊松比 \(\rm nu = 0.3\)
planeStress开关设置为yes,本案例中采用二维平面应力假设。solidDisplacementFoam求解器可以求解热应力方程与动量方程耦合的多物理场传热方程。通过设置thermalStress开关(当前设置为否)来求解热应力方程。此案例中还为钢材指定了热力学属性,即:
比热容 \(\rm Cp=434 Jkg^{-1}·K^{-1} \)
导热系数 \(\rm kappa=60.5 Wm^{-1}·K^{-1} \)
热膨胀系数 \(\rm alphav=1.1\times 10^{-5} K^{-1} \)
对于传热计算,温度场变量 T 存在于 0 目录中。
求解控制
如之前的案例所述,controlDict字典负责读取与求解过程的相关信息。本案例中,开始时间是0秒。由于这是一个稳态案例,因此时间步长并不重要。在这种情况下,推荐将时间步长deltaT设置为1,这样它就只作为稳态案例的迭代计数器。endTime设置为100,作为迭代次数的限制;writeInterval设置为20。
controlDict 字典如下:
16
17application foamRun;
18
19solver solidDisplacement;
20
21startFrom startTime;
22
23startTime 0;
24
25stopAt endTime;
26
27endTime 100;
28
29deltaT 1;
30
31writeControl timeStep;
32
33writeInterval 20;
34
35purgeWrite 0;
36
37writeFormat ascii;
38
39writePrecision 6;
40
41writeCompression off;
42
43timeFormat general;
44
45timePrecision 6;
46
47runTimeModifiable true;
48
49
50// ************************************************************************* //
离散化格式和线性求解器控制
对于fvSchemes字典。首先,该案例为稳态模拟,因此在timeScheme中设置时间导数d2dt2Schemes为SteadyState,实质上这是关闭了时间导数项。并非所有的求解器都适用于稳态和瞬态问题,特别是流体动力学中的求解器。但solidDisplacementFoam均适合稳态和瞬态问题的,因为两种类型的求解基本算法是相同的。
在分析线性弹性应力时,其中的动量方程包括几个含有位移梯度的显性项。仿真计算时,应充分评估梯度较大和较小区域的准确性。通常,在有限体积法中,离散化是基于高斯方法的。对于大多数情况来说,高斯方法足够准确。在本案例中使用最小二乘法。因此,应打开system目录中的fvSchemes字典,并确保为gradSchemes的梯度离散化格式选择了leastSquares方法:
16
17d2dt2Schemes
18{
19 default steadyState;
20}
21
22ddtSchemes
23{
24 default Euler;
25}
26
27gradSchemes
28{
29 default leastSquares;
30}
31
32divSchemes
33{
34 default none;
35 div(sigmaD) Gauss linear;
36}
37
38laplacianSchemes
39{
40 default Gauss linear corrected;
41}
42
43interpolationSchemes
44{
45 default linear;
46}
47
48snGradSchemes
49{
50 default none;
51}
52
53// ************************************************************************* //
system目录中的fvSolution字典用于设置线性方程求解器和算法。首先,solvers子字典中”(D|e)”求解器设置为GAMG。对于本案例,求解器残差应设置为 \(10^{−6}\)。求解器相对残差(用relTol表示)设置了每次迭代中残差所需的减少量。在稳态算法中,在每次迭代中设置严格(低)的相对残差不划算的,这是因为每个方程中的许多项都是明确的,并且会作为分离迭代过程的一部分进行更新。因此,相对残差的合理值为0.01,或者更大,比如0.1,在某些情况下甚至为0.9(如本案例)。
16
17solvers
18{
19 "(D|e)"
20 {
21 solver GAMG;
22 tolerance 1e-06;
23 relTol 0.9;
24 smoother GaussSeidel;
25 nCellsInCoarsestLevel 20;
26 }
27}
28
29PIMPLE
30{
31 compactNormalStress yes;
32}
33
34
35// ************************************************************************* //
运行代码
大家可以尝试在终端后台运行foamRun。在后台运行 OpenFOAM 应用程序时,标准输出(日志信息)应重定向到文件。如下命令将标准输出写入名为 log 的文件中,稍后可以检查该文件。
foamRun > log &
查看生成的log文件来检查收敛信息。终端显示了迭代次数以及每个方向上正在求解的位移初始和最终残差。由于设置了迭代残差,因此最终残差应始终小于初始残差的0.9倍。到计算结束时,初始残差已降低到收敛残差\(10^{−6}\)。
后处理
solidDisplacementFoam求解器将应力场\(\sigma \)输出为对称张量场 sigma。为了对单个标量场分量 \(\sigma _{xx} \), \(\sigma _{xy} \)等进行后处理,使用foamPostProcess程序,并使用-func选项对sigma场调用components函数对象,如下所示:
foamPostProcess -func "components(sigma)"
将名为 sigmaxx、sigmaxy 等的组件写入案例的时间目录中。\(\sigma _{xx} \)应力可以在 ParaView 中查看,如图 2.23 所示:
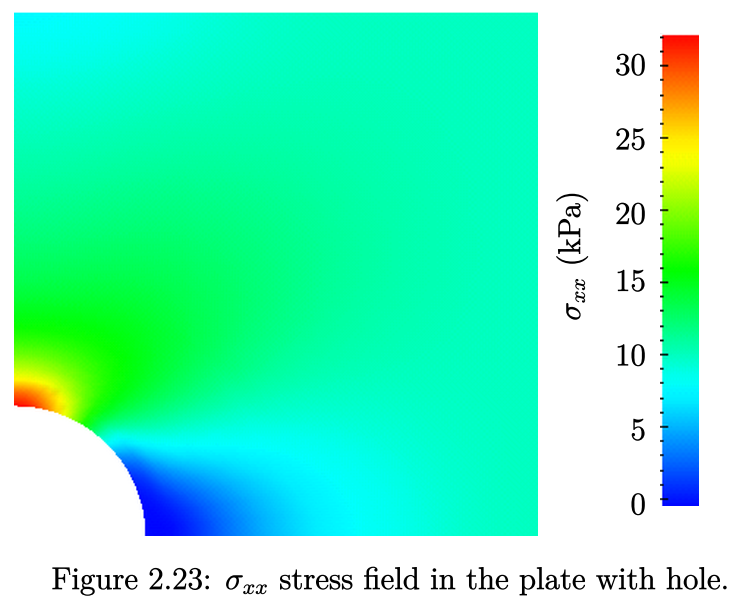
为了将数值解与等式2.7的解析解进行比较,需要沿着域的左边缘对称平面提取\(\sigma _{xx} \)的数据。可以使用带有graphUniform函数的foamPostProcess程序生成所需的图形数据。与之前的foamPostProcess示例(不需要配置)不同,本案例包括在system目录中预先配置的graphUniform文件。采样线设置在(0.0, 0.5, 0.25)和(0.0, 2.0, 0.25)之间,并在fields列表中指定场:
9 Writes graph data for specified fields along a line, specified by start and
10 end points. A specified number of graph points are used, distributed
11 uniformly along the line.
12
13\*---------------------------------------------------------------------------*/
14
15start (0 0.5 0.25);
16end (0 2 0.25);
17nPoints 100;
18
19fields (sigmaxx);
20
21axis y;
22
23#includeEtc "caseDicts/postProcessing/graphs/graphUniform.cfg"
24
25// ************************************************************************* //
使用 graphUniform 函数执行 postProcessing:
foamPostProcess -func graphUniform
数据以raw 2列格式写入到postProcessing/graphUniform目录的时间子目录中的文件内,例如,t=100s时的数据可以在文件graphUniform/100/line.xy中找到。如果安装了GnuPlot,可以通过键入gnuplot启动,然后按照以下方式绘制数值数据和解析解:
plot [0.5:2] [0:] "postProcessing/graphUniform/100/line.xy",
1e4*(1+(0.125/(x**2))+(0.09375/(x**4)))
图 2.24 为示例图。