用户指南:第2章
本案例中,采用不可压缩的VoF模型求解器,求解简化的二维溃坝问题。本案例为瞬态流动,两相流体由一个明确的界面或自由表面分隔开。在incompressibleVoF中,两相算法是以流体体积(VoF)为基础的。在这种算法中,使用相传输方程来确定每个计算单元中各相的相对体积分数,或称为相分数α。根据这个相对体积分数,通过加权平均计算得出材料的物理属性。VoF方法的特性意味着相之间的界面并非显式计算得出,而是作为相分数场的一个特性显现。由于相分数的取值范围在0到1之间,因此不能精确定义相界面,而是占据应存在尖锐界面的区域体积。
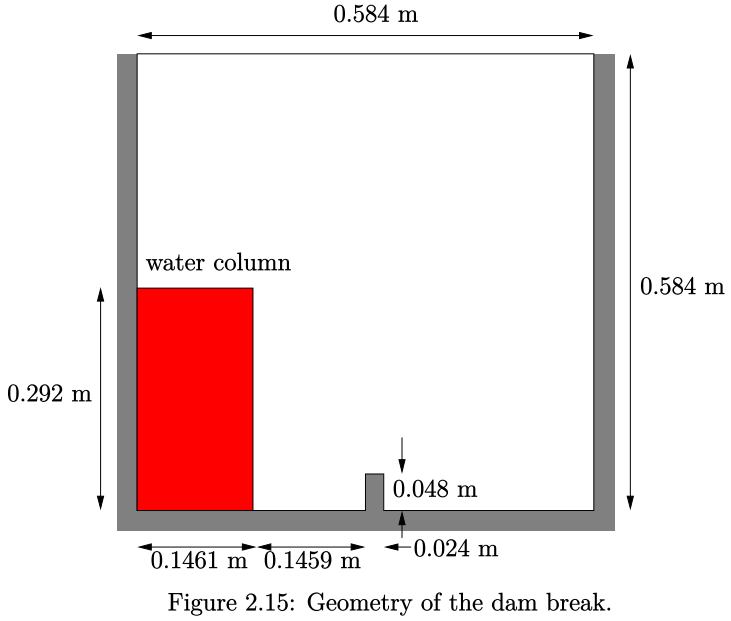
仿真区域由位于水箱左侧隔膜后的一列静止水柱构成。在时间t=0s时刻,移除隔板,水柱崩塌。在崩塌过程中,水冲击水箱底部的障碍物,并产生一个复杂的流场结构,流场中包括几个空气泡。几何模型和初始设置如图2.15所示:
网格生成
打开案例运行目录,并从$FOAM_TUTORIALS/incompressibleVoF/damBreakLaminar目录中复制damBreak案例,即
run
cp -r $FOAM_TUTORIALS/incompressibleVoF/damBreakLaminar/damBreak .
进入damBreak文件夹,然后运行blockMesh以生成网格。damBreak网格由五个block构成,blockMeshDict的相关条目如下所示。
16convertToMeters 0.146;
17
18vertices
19(
20 (0 0 0)
21 (2 0 0)
22 (2.16438 0 0)
23 (4 0 0)
24 (0 0.32876 0)
25 (2 0.32876 0)
26 (2.16438 0.32876 0)
27 (4 0.32876 0)
28 (0 4 0)
29 (2 4 0)
30 (2.16438 4 0)
31 (4 4 0)
32 (0 0 0.1)
33 (2 0 0.1)
34 (2.16438 0 0.1)
35 (4 0 0.1)
36 (0 0.32876 0.1)
37 (2 0.32876 0.1)
38 (2.16438 0.32876 0.1)
39 (4 0.32876 0.1)
40 (0 4 0.1)
41 (2 4 0.1)
42 (2.16438 4 0.1)
43 (4 4 0.1)
44);
45
46blocks
47(
48 hex (0 1 5 4 12 13 17 16) (23 8 1) simpleGrading (1 1 1)
49 hex (2 3 7 6 14 15 19 18) (19 8 1) simpleGrading (1 1 1)
50 hex (4 5 9 8 16 17 21 20) (23 42 1) simpleGrading (1 1 1)
51 hex (5 6 10 9 17 18 22 21) (4 42 1) simpleGrading (1 1 1)
52 hex (6 7 11 10 18 19 23 22) (19 42 1) simpleGrading (1 1 1)
53);
54
55defaultPatch
56{
57 type empty;
58}
59
60boundary
61(
62 leftWall
63 {
64 type wall;
65 faces
66 (
67 (0 12 16 4)
68 (4 16 20 8)
69 );
70 }
71 rightWall
72 {
73 type wall;
74 faces
75 (
76 (7 19 15 3)
77 (11 23 19 7)
78 );
79 }
80 lowerWall
81 {
82 type wall;
83 faces
84 (
85 (0 1 13 12)
86 (1 5 17 13)
87 (5 6 18 17)
88 (2 14 18 6)
89 (2 3 15 14)
90 );
91 }
92 atmosphere
93 {
94 type wall;
95 faces
96 (
97 (8 20 21 9)
98 (9 21 22 10)
99 (10 22 23 11)
100 );
101 }
102);
103
104
105// ************************************************************************* //
网格信息保存在constant目录下的polyMesh文件夹内的多个文件中。可以输入如下命令,列出该文件夹下的子文件,并查看:
ls constant/polyMesh
polyMesh文件夹包含如下文件:boundary(对边界域集合的描述)、faces(单元格面的列表)、neighbour和owner(包含与特定面相连的单元格索引)、points(单元格顶点的列表)。
边界条件
boundary文件的内容是可读的,可以使用文件编辑器打开,或使用cat工具在终端窗口中输出其内容。cat工具命令如下:
cat constant/polyMesh/boundary
该文件包含了五个边界,分别是:leftWall、rightWall、lowerWall、atmosphere以及defaultFaces。值得注意,关注这些边界的类型是必要的。
首先,atmosphere是一个标准的patch,即它不具备任何特殊属性,仅仅是一个用来指定边界条件的单元。 其次,defaultFaces是由在blockMeshDict文件的boundary子字典中被省略的区所构成的,这些被省略的区块共同组成了一个patch,其相关属性在blockMeshDict文件中的defaultPatch子字典里进行了详细规定。本案例中,由于该patch的法线方向是在这个二维案例中无法求解的方向,因此默认类型设置为空。
leftWall、rightWall和lowerWall边界均设定为wall类型。与通用的patch相似,wall类型不包含任何关于网格的几何或拓扑信息。它与标准的patch的区别仅在于,wall类型将区块标识为壁面。这对于特定模型来说是必要的,例如湍流壁函数,还有一些在计算中需要考虑距最近壁面距离的湍流模型。
defaultFaces边界代表二维域的前后平面,与atmosphere一样,是一个空类型。 特别是在VOF模拟中,表面张力模型可以模拟界面与壁面接触点之间的壁面粘附效应。壁面粘附模型可通过在alpha(α)场上应用特定的边界条件来实现,例如使用constantAlphaContactAngle边界条件,此时需要设定一个静态接触角theta0。
本例忽略壁面与界面之间的表面张力效应。要实现这一点,一种方法是设置静态接触角\(\theta _{0} =90^{\circ} \),另一种方法是在壁面上对alpha应用zeroGradient条件。
顶部边界与大气相通,因此需根据内部流动情况允许同时存在流出和流入。为了实现这一点并保持流动稳定性,需要将压力和速度的边界条件相结合。这些边界条件包括:
prghTotalPressure 这一边界条件应用于压力场,但要减去由公式6.3给出的静水压分量 \(p_{\rho gh} \);
pressureInletOutletVelocity这一边界条件应用于速度U,该条件会对速度U的所有分量设置zeroGradient(零梯度),但在流入区域,则对切向分量应用fixedValue(固定值)条件;
inletOutlet 这一边界条件应用于其他场,在向外流动时表现为zeroGradient条件,在向内流动时表现为fixedValue条件。
在所有壁面边界上,fixedFluxPressure边界条件应用于压力场,并通过调整压力梯度,使边界通量与求解器(包括重力和表面张力等体力)的速度边界条件相匹配。
相
流体相的具体信息在constant目录下的phaseProperties文件中指定。phaseProperties文件内容如下所示:
16
17phases (water air);
18
19sigma 0.07;
20
21
22// ************************************************************************* //
第17行列出了液相和气相。除了列表中的最后一个相(本例中是气相)之外,系统会为列表中的其它相求解相分数方程。由于这里只有两个相,所以只会为第一个相分数方程求解,即求解液相分数 \(\alpha _{water}\),具体数值在0目录下的alpha.water文件中指定。
PhaseProperties文件包含两相之间的表面张力,由关键字sigma指定,单位为 \(\rm N·m^{-1} \)。
设定初始场
与上文的案例不同,如下案例将为相分数 \(\alpha _{water}\) 指定一个非均匀初始条件,其中:
这可以通过运行setFields来实现。运行该工具需要一个位于system目录下的setFieldsDict字典,针对本案例的字典条目如下所示。
16
17defaultFieldValues
18(
19 volScalarFieldValue alpha.water 0
20);
21
22regions
23(
24 boxToCell
25 {
26 box (0 0 -1) (0.1461 0.292 1);
27 fieldValues
28 (
29 volScalarFieldValue alpha.water 1
30 );
31 }
32);
33
34
35// ************************************************************************* //
defaultFieldValues用于设定场的默认值,即在regions列表中没有特别指定时,场采用默认值。regions列表中包含一些带有fieldValues的子字典,这些子字典会在特定区域内覆盖默认值。区域是通过定义一组点、面或单元的函数来确定的。在本算例中,boxToCell函数创建了一个由最小和最大边界定义的区域,这个区域定义了液相域的单元集。在这个区域内,液相分数\(\alpha _{water}\)设定为1。
setFields工具从文件中读取各种场信息,重新计算这些场之后,将场信息写回文件。在本案例中,alpha.water场最初以原始形式存储,并命名为alpha.water.orig。如果实际的目标文件不存在,程序会读取带有.orig扩展名的场文件。因此,setFields会读取alpha.water.orig文件,但将输出结果写入alpha.water文件(如果启用压缩功能,则写入alpha.water.gz文件)。通过这种方式,原始文件不会被覆盖,可以重复使用。
执行如下命令:
setFields
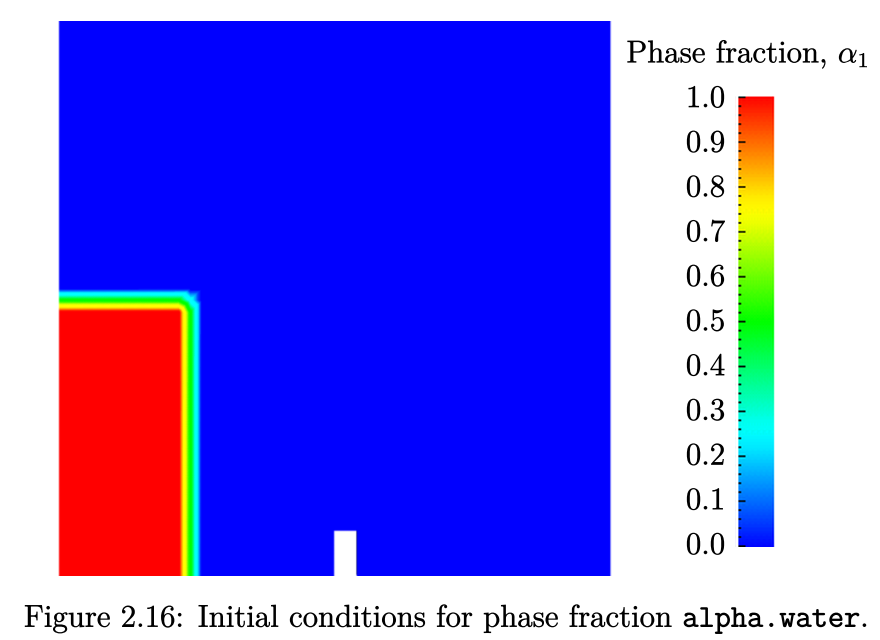
使用 paraFoam,检查初始 alpha.water 场是否对应于所需的分布,如图2.16所示。
属性
气相和液相的物理特性分别在constant目录下的physicalProperties.air和physicalProperties.water文件中设置。这2个文件描述了流体在静止情况下的物理性质。并且,通过viscosityModel关键字指定粘度模型,该关键字设置为constant,表示该值是恒定的。然后,通过nu关键字以 \(\rm m^{2}·s^{-1} \) 为单位指定粘度。流体的密度也以 \(kg·m^{-3}\) 为单位通过rho关键字指定。下面以physicalProperties.air文件为例:
16
17viscosityModel constant;
18
19nu 1.48e-05;
20
21rho 1;
22
23
24// ************************************************************************* //
如果粘度随剪切速率而变化,如非牛顿或粘弹性流体,则通过动量属性文件指定粘度模型,见后文第 8.3 节。
重力
整个区域内重力加速度是均匀的,并由constant目录中的g文件夹指定。与常规场文件(如U和p)不同,g是一个uniformDimensionedVectorField,因此它只包含一组维度和一个值,对于本算例来说,它代表(0, -9.81, 0) \(\rm m·s^{-2} \):
16
17dimensions [0 1 -2 0 0 0 0];
18value (0 -9.81 0);
19
20
21// ************************************************************************* //
湍流模型
与cavity案例相同,可以通过momentumTransport字典中的simulationType关键字来设置湍流模型。在本案例中,假定流动过程没有涡旋,因此设置为层流:
16
17simulationType laminar;
18
19
20// ************************************************************************* //
时间步长控制
溃坝案例是瞬态仿真,因此需要注意时间步长的设定。库朗数Co(Courant number)与时间步长相关,是针对每个单元定义的无量纲参数,定义为:
其中, \(\delta t\)是时间步长,\(\left | \bfU \right |\) 是通过该单元的速度大小,\(\delta x\) 是速度方向上的单元大小。对于显式求解,为了保持稳定性,需要满足最大Co小于1;更严格的稳定性限制取决于流体流动模型的选择。通常,隐式求解没有固定的最大库朗数稳定性限制,但当Co超过1时,时间精度将变得更加重要。
时间步长对于界面捕捉尤为重要。incompressible Volume of Fluid求解器模块使用了由Henry Weller创建的Multidimensional Universal Limiter for Explicit Solution (MULES),以保持相分数的有界性。根据所选的MULES算法,需要对库朗数进行限制。使用最初的显式MULES算法时,为了保持稳定,通常需要将库朗数的上限为 \(Co\approx 0.25\)。并且,还有一种半隐式的MULES算法,可通过在fvSolution文件中使用MULESCorr开关来指定。对于半隐式MULES算法,Co的稳定性没有上限值,而是根据时间精度的要求来决定的。
一般来说,很难指定一个固定的时间步长来满足Co标准。因为在仿真过程中,\(\left | \bfU \right |\)会随着单元的变化而变化。对于自动调整时间步长,需要将controlDict中的adjustTimeStep切换为on,并指定相场和其他场的最大库朗数maxAlphaCo和maxCo。在本例中,maxAlphaCo和maxCo都设置为1.0。时间步长的上限maxDeltaT,可以设置为本案例中不会超过的值,例如1.0。
当使用自动时间步长,时间步长本身不会被四舍五入。因此,OpenFOAM可按需要以固定的时间步长间隔保存结果。但是,通过调整自动时间步长,可以使用controlDict字典中writeControl的可调整adjustableRunTime选项在固定时间保持结果。使用该选项,自动时间步长程序会进一步调整其时间步长,以便在writeInterval指定的确切时间“命中”,本例中设置为0.05。,controlDict文件位于system文件夹中,其字典条目如下所示。
16
17application foamRun;
18
19solver incompressibleVoF;
20
21startFrom startTime;
22
23startTime 0;
24
25stopAt endTime;
26
27endTime 1;
28
29deltaT 0.001;
30
31writeControl adjustableRunTime;
32
33writeInterval 0.05;
34
35purgeWrite 0;
36
37writeFormat binary;
38
39writePrecision 6;
40
41writeCompression off;
42
43timeFormat general;
44
45timePrecision 6;
46
47runTimeModifiable yes;
48
49adjustTimeStep yes;
50
51maxCo 1;
52maxAlphaCo 1;
53
54maxDeltaT 1;
55
56
57// ************************************************************************* //
离散化
incompressibleVoF求解器所使用的MULES算法独立于底层数值方案、网格结构等来保持相分数的有界性。因此,对流方案的选择并不局限于那些强稳定或有界的方案,如upwind。
在 fvSchemes 字典的 divSchemes 子字典中,设置对流相离散化方案。本案例中,动量方程中的对流项 \(\nabla \cdot \left ( \rho \rm UU \right ) \)(用 div(rhoPhi,U) 表示)使用Gauss linearUpwind grad(U),并获得较好的离散化效果。
\(\nabla \cdot \left ( \rm U\alpha \right ) \) 项由div(phi,alpha)表示,使用了一种定制的interfaceCompression方法。其中,vanLeer系数是一个控制界面压缩的因子,具体为:0表示不压缩;1表示保守压缩;大于1的任何值则表示增强界面的压缩。通常使用的值为1.0,如本案例所示。
其它离散项使用常用的方案,因此fvSchemes字典条目如下所示。
16
17ddtSchemes
18{
19 default Euler;
20}
21
22gradSchemes
23{
24 default Gauss linear;
25}
26
27divSchemes
28{
29 div(rhoPhi,U) Gauss linearUpwind grad(U);
30 div(phi,alpha) Gauss interfaceCompression vanLeer 1;
31 div(((rho*nuEff)*dev2(T(grad(U))))) Gauss linear;
32}
33
34laplacianSchemes
35{
36 default Gauss linear corrected;
37}
38
39interpolationSchemes
40{
41 default linear;
42}
43
44snGradSchemes
45{
46 default corrected;
47}
48
49
50// ************************************************************************* //
矩阵求解器
在system/fvSolution文件中,solvers内用于alpha.water的子字典包含特定于MULES算法的元素,如下所示。
"alpha.water.*"
{
nAlphaCorr 2;
nAlphaSubCycles 1;
MULESCorr yes;
nLimiterIter 5;
solver smoothSolver;
smoother symGaussSeidel;
tolerance 1e-8;
relTol 0;
}
MULES通过计算两个限制器来将相分数保持在0和1之间。限制器的是迭代计算的,迭代次数由nLimiterIter指定。根据经验,可以将nLimiterIter设置为3 + ,以保持Co数的有界性。
通过MULESCorr开关可以激活MULES的半隐式算法。在应用MULES作为高阶校正之前,首先需要计算出一个隐式格式的迎风解。然后,需要通过solver, smoother, tolerance 和 relTol等参数,为隐式迎风解配置线性求解器。
nAlphaCorr 关键字用于控制一个解步骤中相分数方程的迭代次数。迭代用于克服对流中的非线性,在这种情况下,非线性是由interfaceCompression方案引起的。
运行代码
代码的运行已在前面的教程中进行了叙述。尝试以下使用 tee 的命令,该命令允许将输出写入标准输出和文件
cd $FOAM_RUN/damBreak
foamRun | tee log
现在采用交互式运行代码,并将输出的副本存储在log文件中。
后处理
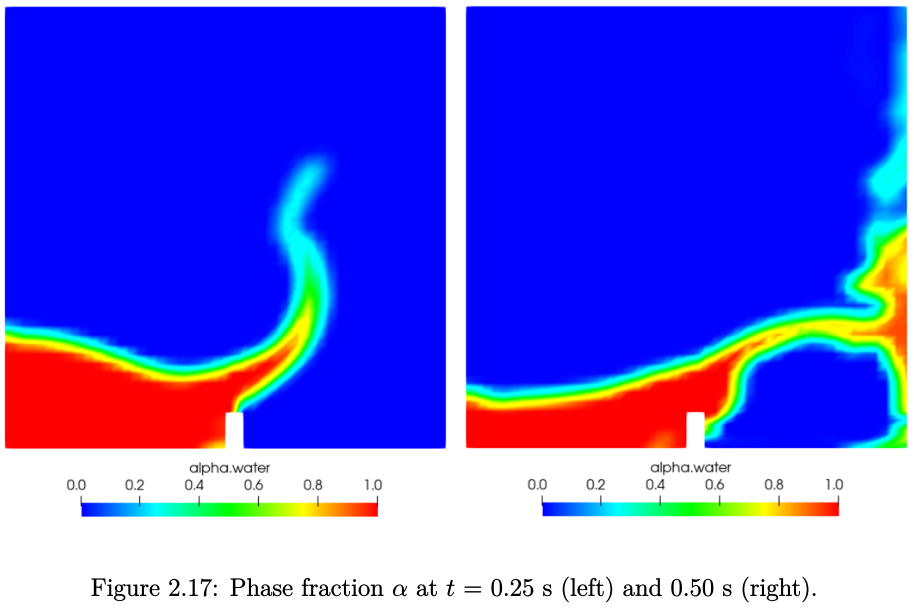
现在可按常用的方式对结果进行后处理。用户可以及时监测相分数alpha.water的变化情况,例如下图:
并行运行
上一个示例的结果是使用相对粗糙网格生成的, 现在希望增加网格分辨率并重新计算。 使用更精细的网格进而展示 OpenFOAM 的并行处理能力。
首先复制damBreak案例,例如
run
foamCloneCase damBreak damBreakFine
进入新的case目录(路径:run/damBreakFine/system/),将blockMeshDict字典中的块描述更改为
blocks
(
hex (0 1 5 4 12 13 17 16) (46 10 1) simpleGrading (1 1 1)
hex (2 3 7 6 14 15 19 18) (40 10 1) simpleGrading (1 1 1)
hex (4 5 9 8 16 17 21 20) (46 76 1) simpleGrading (1 2 1)
hex (5 6 10 9 17 18 22 21) (4 76 1) simpleGrading (1 2 1)
hex (6 7 11 10 18 19 23 22) (40 76 1) simpleGrading (1 2 1)
);
此处显示从 blockMeshDict 文件中摘取的内容。需要更改设置以调整网格密度,例如设置 (46 10 1) 和 (1 2 1)。随后,运行 blockMesh 生成网格。
由于对网格进行了修改,因此damBreakFine案例里包含一些与新网格不一致的元素,所以需要在0时间目录中重新初始化相场alpha.water。需要注意,因为U和p_rgh场指定为均一值,与场中的单元数量无关,所以U和p_rgh场不需更改。
然后,重新运行setFields。首先,由于现在的网格大小与0目录中alpha.water文件中的元素数量不一致,必须删除alpha.water文件,以便setFields使用原始的alpha.water.orig文件。
rm 0/alpha.water
setFields
使用区域分解法进行并行计算。其中,将几何形状和相关场分解成多个部分,并分配给单独的处理器进行求解。因此,运行并行案例的第一步是使用decomposePar程序对区域进行分解。与decomposePar相关的是名为decomposeParDict的字典,其位于system目录中。此外,OpenFOAM中的etc目录中也可以找到案例字典,可以通过运行foamGet脚本将其复制到案例目录中:
foamGet decomposeParDict
输入上面命令后弹出下列内容:
Multiple files with "decomposeParDict" prefix found:
1) /home/dyfluid/OpenFOAM/OpenFOAM-11/etc/caseDicts/annotated/decomposeParDict
2) /home/dyfluid/OpenFOAM/OpenFOAM-11/etc/caseDicts/preProcessing/decomposeParDict
** Note: it is easier to use files NOT in the "annotated" directory
Enter file number (1-2) to obtain description (suggest 2) : 2
Copying /home/dyfluid/OpenFOAM/OpenFOAM-11/etc/caseDicts/preProcessing/decomposeParDict to system
*****************************
建议输入2。然后再system文件夹下面,会出现decomposeParDict的字典。其中的numberOfSubdomains指定案例分解成子域的数量,通常与可用的处理器数量相对应。比如2个核求解,numberOfSubdomains=2;8个核求解,numberOfSubdomains=8。
本案例使用simple method。它需要根据以下步骤来常规配置simpleCoeffs。域在x、y和z方向上分割成多个部分或子域,每个方向上的子域数量由向量n给出。由于此几何形状是二维的,因此第三个方向z无法分割,所以 \(n_z\)等于1。n的\(n_x\)和\(n_y\)分量必须指定在x和y方向上分割域,这样\(n_x\)和\(n_y\)指定的子域数量可以等于指定的numberOfSubdomains,即\(n_xn_y\) = numberOfSubdomains。
推荐将与子域相邻的单元面的数量保持在最低限度,因此对于方形几何形状,最好保持x和y方向之间的分割均匀。例如,假设希望在4个处理器上运行。会将numberOfSubdomains设置为4,n设置为(2, 2, 1)。用户应通过以下命令运行decomposePar。
decomposePar
终端输出显示分解的子域之间为均匀分布。分解将每个子域的网格和字段写入名为processor
本案例展示了使用标准message-passing interface(MPI)的openMPI执行并行计算。若要使用多核心CPU的4个内核执行并行计算,可运行以下命令。
mpirun -np 4 foamRun -parallel
有关如何并行运行案例的更多详细信息,可以查阅第 3.4 节获取。例如,通过创建一个文件在网络上的更多节点上运行,该文件列出了要运行案例的机器的主机名,见第 3.4.3 节。
对并行计算的案例进行后处理
当案例并行运行时,结果将写入到processor
ls processor0
通过将单独的处理器目录视为一个独立的案例,进而对单个子域进行后处理。例如,要在ParaView中查看processor1子域,运行以下命令来启动paraFoam:
paraFoam -case processor1
图 2.18 显示该子域的网格,使用simple方法对域进行分解。

或者,对分解后的场和网格进行重新组合,以便进行串行后处理。reconstructPar工具从处理器子域的时间目录中获取字段文件,并为整个域构建等效的场文件。运行如下命令:
reconstructPar
重构后的场被写入案例目录中的解决方案时间目录。这些字段可以在ParaView中正常可视化。细网格的结果如图2.19所示。可以看到,与粗网格相比,气液界面的分辨率有了显著提高。