ML: 反向传播与自动微分
在阅读本文之前,请阅读《无痛苦NS方程笔记》中的监督学习的数学算法一节。在构建神经网络后,通常采取反向传播的方法来计算对权重以及偏置的梯度。本文以一个实例来解释反向传播的梯度计算方法。
反向传播

在上图中,假定输入层有两个变量\(x,y\),每个变量仅仅存在一个特征,\(x=3,y=4\)。隐藏层存在2个ReLU神经元。输出层的值是yIter。同时,每个神经元的权重、偏置已经给出。下面我们要通过反向传播的方法来更新权重与偏置。
首先计算神经元\(a_1\)的值:
(1)\[
a_1=\max (0, w_{11}x+w_{21}y+b_1)=\max (0, 0.9\cdot 3+0.7\cdot 4+0.5)=6
\]
然后计算神经元\(a_2\)的值:
(2)\[
a_1=\max (0, w_{12}x+w_{22}y+b_2)=\max (0, 0.8\cdot 3+0.6\cdot 4+0.5)=5.3
\]
计算预测的yIter的值:
(3)\[
y_{iter}=\max (0, w'_{1}a_1+w'_{2}a_2+b')= 2.96
\]
假定真实的\(y\)值是1,目前可以计算损失:
(4)\[
loss=\frac{1}{2}(y-y_{iter})^2=1.92
\]
反向传播主要是通过算法求解出\(\frac{\p loss}{\p w'_1}\),然后更新\(w'_1\)。这里的\(w'_1\)只是一个具体的例子,对于所有的权重都需要这样去更新。那么如何求解出\(\frac{\p loss}{\p w'_1}\)?反向传播主要使用的数学思想是链式法则:
(5)\[
\frac{\p loss}{\p w'_1}=\frac{\p loss}{\p y_{iter}} \frac{\p y_{iter}}{\p w'1}
\]
从方程(4)中可以看出:
(6)\[
\frac{\p loss}{\p y_{iter}} = y_{iter}-y=1.96
\]
从方程(3)中可以看出:
(7)\[
\frac{\p y_{iter}}{\p w'1}= a_1=5.3
\]
因此有:
(8)\[
\frac{\p loss}{\p w'_1}=1.96\cdot 5.3 = 10.388
\]
类似的,针对\(w_{11}\),有:
(9)\[
\frac{\p loss}{\p w_{11}}=\frac{\p loss}{\p y_{iter}} \frac{\p y_{iter}}{\p a_1} \frac{\p a_1}{\p w_{11}}
\]
其中
(10)\[
\frac{\p y_{iter}}{\p a_1} =w'_1=0.3
\]
(11)\[
\frac{\p a_1}{\p w_{11}}=x=3
\]
于是有:
(12)\[
\frac{\p loss}{\p w_{11}}=1.96\cdot 0.3 \cdot 3 = 1.764
\]
Warning
在这里要注意,方程(12)在计算损失的时候,乘以了\(w'_1\)的数值。也就是说计算前一层的梯度的时候,需要调用后一层的权重值。在极端情况下,比如\(w'_1=0\),那么这个导数就成为了\(0\)。也即梯度消失。
同理,针对\(w_{12}\),有:
(13)\[
\frac{\p loss}{\p w_{12}}=\frac{\p loss}{\p y_{iter}} \frac{\p y_{iter}}{\p a_1} \frac{\p a_1}{\p w_{12}}=1.96\cdot 0.3 \cdot 4=2.352
\]
其他权重以及偏置的计算方法完全相同。本算例中的参数向量假定为\(\boldsymbol{\theta}\):
(14)\[\begin{split}
\boldsymbol{\theta}=
\begin{bmatrix}
w_{11}\\
w_{12}\\
w_{21}\\
w_{22}\\
w'_{1}\\
w'_{2}\\
b_1\\
b_2\\
b'
\end{bmatrix}
\end{split}\]
梯度下降方法需要计算出所有的导数:
(15)\[\begin{split}
\frac{\p loss}{\p \boldsymbol{\theta}}=
\begin{bmatrix}
\frac{\p loss}{\p w_{11}}\\
\frac{\p loss}{\p w_{12}}\\
\frac{\p loss}{\p w_{21}}\\
\frac{\p loss}{\p w_{22}}\\
\frac{\p loss}{\p w'_{1}}\\
\frac{\p loss}{\p w'_{2}}\\
\frac{\p loss}{\p b_1}\\
\frac{\p loss}{\p b_2}\\
\frac{\p loss}{\p b'}
\end{bmatrix}
\end{split}\]
在上文中,我们已经演示了反向传播计算导数的方法,假定方程(15)中的导数已经全部计算出。下一步更新梯度的时候,就成为:
(16)\[\begin{split}
\boldsymbol{\theta}^{new}=
\begin{bmatrix}
w_{11}\\
w_{12}\\
w_{21}\\
w_{22}\\
w'_{1}\\
w'_{2}\\
b_1\\
b_2\\
b'
\end{bmatrix}
-\alpha \begin{bmatrix}
\frac{\p loss}{\p w_{11}}\\
\frac{\p loss}{\p w_{12}}\\
\frac{\p loss}{\p w_{21}}\\
\frac{\p loss}{\p w_{22}}\\
\frac{\p loss}{\p w'_{1}}\\
\frac{\p loss}{\p w'_{2}}\\
\frac{\p loss}{\p b_1}\\
\frac{\p loss}{\p b_2}\\
\frac{\p loss}{\p b'}
\end{bmatrix}
\end{split}\]
计算导数与更新参数:
方程(15)对应伪代码loss.backward();方程(15)对应伪代码adam->step();
其中\(\alpha\)是学习率,是一个超参数(用户自定义参数)。有两点需要注意:
自动微分

现在将上图复制一遍贴在这里,还是以这个图来距离。一些情况下(例如如果使用PINN求解PDE的情况下),不仅需要求对权重的导数,还需要求对\(x\)或\(y\)的导数。类似上文讨论的反向传播,预测值对\(x\)的导数可以这样求:
(17)\[
\frac{\p y_{iter}}{\p x}=\frac{\p y_{iter}}{\p a_1} \frac{\p a_1}{\p x} + \frac{\p y_{iter}}{\p a_2} \frac{\p a_2}{\p x}=0.3\cdot 0.9+0.2\cdot0.8=0.43
\]
方程(17)很明显是先计算后面的导数然后再往前计算,因此也可以近似理解为后向传播。不过在对变量求导数的时候,这种求法一般被称之为后向模式。另一方面,其还有另外一种求法。这一种方法来起来是从前向后来计算的。从公式上来看也比较好理解:
(18)\[\begin{split}
\frac{\p y_{iter}}{\p x}=
\left( \frac{\p a_1 }{\p x } \frac{\p x }{\p x } + \frac{\p a_1}{\p y} \frac{\p y}{\p x} \right)\frac{\p y_{iter}}{\p a_1}
+
\left( \frac{\p a_2 }{\p x } \frac{\p x }{\p x } + \frac{\p a_2}{\p y} \frac{\p y}{\p x} \right)\frac{\p y_{iter}}{\p a_2}
\\\\
=\left( 0.9 \cdot 1 + 0.7 \cdot 0 \right)\cdot 0.3
+
\left( 0.8\cdot 1 + 0.6 \cdot 0 \right)\cdot 0.2
\\\\
=0.43
\end{split}\]
方程(18)在计算的时候,需要从\( \frac{\p a_1 }{\p x } \)开始,逐步的向后来计算,最终得到一个\(\frac{\p y_{iter}}{\p x}\)。这是另外一种方法,被称之为前向模式。不管是后向模式还是 前向模式,都是计算对\(x\)导数的一种方法,这种方法就是自动微分方法。
针对自动微分的后向模式与前向模式,很明显后向模式需要调用更少的计算次数。因此通常自动微分采用后向模式来进行计算。后向模式自动微分与后向传播的差异更小。后向模式自动微分更像是一种数学方法。后向传播通常值得是针对损失标量,求取对参数向量的梯度的过程,其会调用后向模式自动微分这种数学方法来进行计算。
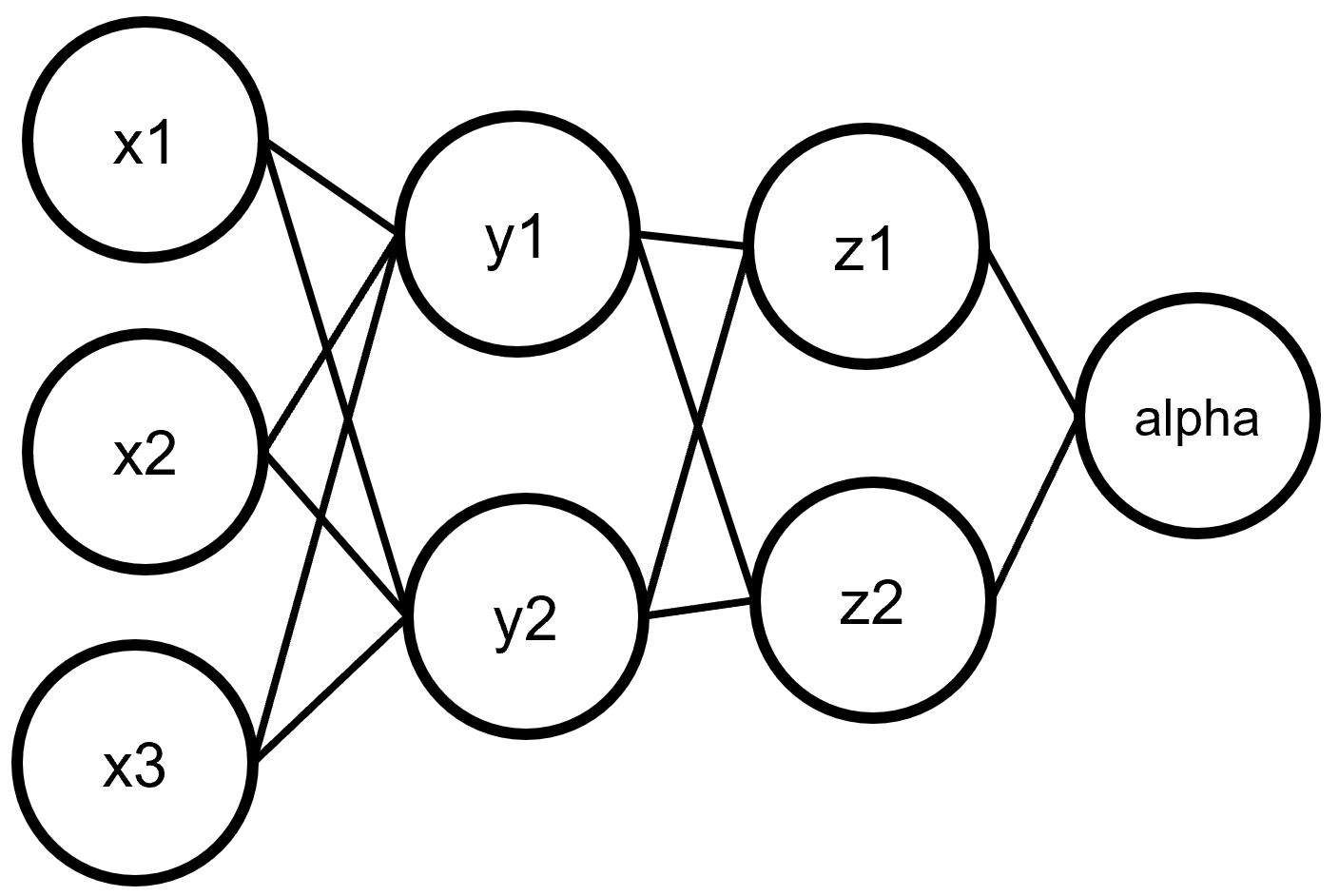
下面进行一个复杂点的计算。给定上图这个神经网络,如何通过后向模式自动微分来计算\( \frac{\p \alpha}{\p x_1} \)(在PINN中这种求导很常见)。首先对于\(x_1,x_2,x_3\)与\(y_1,y_2\)的关系,有转置的雅可比矩阵为:
(19)\[\begin{split}
{\mathbf J}^T({\mathbf y})=\begin{bmatrix}
\frac{\p y_1}{\p x_{1}},\frac{\p y_2}{\p x_{1}}\\
\frac{\p y_1}{\p x_{2}},\frac{\p y_2}{\p x_{2}}\\
\frac{\p y_1}{\p x_{3}},\frac{\p y_2}{\p x_{3}}
\end{bmatrix}
\end{split}\]
对于\(y_1,y_2\)与\(z_1,z_2\)的关系,有转置的雅可比矩阵为:
(20)\[\begin{split}
{\mathbf J}^T({\mathbf z})=\begin{bmatrix}
\frac{\p z_1}{\p y_{1}},\frac{\p z_2}{\p y_{1}}\\
\frac{\p z_1}{\p y_{2}},\frac{\p z_2}{\p y_{2}}
\end{bmatrix}
\end{split}\]
对于\(z_1,z_2\)与\(\alpha\)的关系,有转置的雅可比矩阵为:
(21)\[\begin{split}
{\mathbf J}^T({\mathbf \alpha})=\begin{bmatrix}
\frac{\p \alpha}{\p z_{1}}\\
\frac{\p \alpha}{\p z_{2}}
\end{bmatrix}
\end{split}\]
如果进行这样的计算:
(22)\[\begin{split}
\left(
{\mathbf J}^T({\mathbf y})
\cdot
{\mathbf J}^T({\mathbf z})
\right)
\cdot
{\mathbf J}^T({\mathbf \alpha})
=
\left(
\begin{bmatrix}
\frac{\p y_1}{\p x_{1}},\frac{\p y_2}{\p x_{1}}\\
\frac{\p y_1}{\p x_{2}},\frac{\p y_2}{\p x_{2}}\\
\frac{\p y_1}{\p x_{3}},\frac{\p y_2}{\p x_{3}}
\end{bmatrix}
\cdot
\begin{bmatrix}
\frac{\p z_1}{\p y_{1}},\frac{\p z_2}{\p y_{1}}\\
\frac{\p z_1}{\p y_{2}},\frac{\p z_2}{\p y_{2}}
\end{bmatrix}
\right)
\cdot
\begin{bmatrix}
\frac{\p \alpha}{\p z_{1}}\\
\frac{\p \alpha}{\p z_{2}}
\end{bmatrix}
\\\\
=
\left(
\begin{bmatrix}
\frac{\p y_1}{\p x_{1}}\frac{\p z_1}{\p y_{1}}+\frac{\p y_2}{\p x_{1}}\frac{\p z_1}{\p y_{2}},\frac{\p y_1}{\p x_{1}}\frac{\p z_2}{\p y_{1}}+\frac{\p y_2}{\p x_{1}}\frac{\p z_2}{\p y_{2}}\\
\frac{\p y_1}{\p x_{2}}\frac{\p z_1}{\p y_{1}}+\frac{\p y_2}{\p x_{2}}\frac{\p z_1}{\p y_{2}},\frac{\p y_1}{\p x_{2}}\frac{\p z_2}{\p y_{1}}+\frac{\p y_2}{\p x_{2}}\frac{\p z_2}{\p y_{2}}\\
\frac{\p y_1}{\p x_{3}}\frac{\p z_1}{\p y_{1}}+\frac{\p y_2}{\p x_{3}}\frac{\p z_1}{\p y_{2}},\frac{\p y_1}{\p x_{3}}\frac{\p z_2}{\p y_{1}}+\frac{\p y_2}{\p x_{3}}\frac{\p z_2}{\p y_{2}}
\end{bmatrix}
\right)
\cdot
\begin{bmatrix}
\frac{\p \alpha}{\p z_{1}}\\
\frac{\p \alpha}{\p z_{2}}
\end{bmatrix}
\\\\
=
\begin{bmatrix}
\frac{\p z_1}{\p x_{1}},\frac{\p z_2}{\p x_{1}}\\
\frac{\p z_1}{\p x_{2}},\frac{\p z_2}{\p x_{2}}\\
\frac{\p z_1}{\p x_{3}},\frac{\p z_2}{\p x_{3}}
\end{bmatrix}
\cdot
\begin{bmatrix}
\frac{\p \alpha}{\p z_{1}}\\
\frac{\p \alpha}{\p z_{2}}
\end{bmatrix}
=\begin{bmatrix}
\frac{\p \alpha}{\p x_{1}} \\
\frac{\p \alpha}{\p x_{2}} \\
\frac{\p \alpha}{\p x_{3}}
\end{bmatrix}
\end{split}\]
可以看出,方程(22)就是\(\alpha\)对\(\mathbf x\)的导数。
(23)\[
\frac{\p \alpha}{\p \mathbf x}
=
\left(
{\mathbf J}^T({\mathbf y})
\cdot
{\mathbf J}^T({\mathbf z})
\right)
\cdot
{\mathbf J}^T({\mathbf \alpha})
\]
方程(23)就是自动微分计算导数的方法。