版本对应：

本网页讨论的机器学习内容，为特定的机器学习内容（并未与CFD结合）。在《无痛苦NS方程笔记》中， 特定的将CFD与机器学习互相结合起来，无普适性机器学习内容。

ML: 卷积神经网络

在阅读本文之前，请阅读《无痛苦NS方程笔记》中的监督学习的数学算法一节。

卷积神经网络在提出的时候主要用于图像识别且目前依然被大量的用于图像识别[LBD+89, LBBH98]。在卷积神经网络提出的基础之上，残差神经网络的提出可以处理太多层的神经网络难以训练的问题（该论文于2016年发表，目前被引用20万次）[HZRS16]。卷积神经网络在一些工作中被用于CFD的流场快速预测[GLI16, SJSK19] 。残差神经网络也被一些工作中作为一种数据驱动的湍流模型被应用于流场计算中[BFM19]。本文讨论卷积神经网络与残差神经网络的基本原理，具体的与CFD方向的结合，请参考《无痛苦NS方程笔记》。

卷积神经网络可以看做一个思想。其可以应用于很多其他方面。后续还会介绍编码器与解码器。读者会发现大体类似。

考虑上面一个2D的流场切面（红色的可能表示相分数），其可以看做由若干个网格点组成。每个网格点上定义着变量的具体的值。如果我们考虑速度。因为速度具有2个分量，因此每个网格上存在2个速度的分量值。在全连接网络中，考虑\(u\)速度分量，所有的网格的\(u\)的值可以展平（Flatten）成一个列向量，同时所有的网格的\(v\)的值可以展平成一个列向量。在输入到神经网络之前，两个列向量要进行拼接（Concatenate）形成一个特别长的输入层。后面连接的为隐藏层以及输出层。针对全连接网格，如果我们的2D网格有1000个网格单元。拼接后输入层的元素有2000个（单单这一个流场切片）。如果隐藏层有20个神经元，那么权重的数量为\(2000\times 20\)，共4万个。如果附加更多的隐藏层，会存在更多更多的权重。这有2方面弊端：1）未知参数太多，训练较慢。2）过多的参数确实可以捕获各种流场细节（例如如果进行流场涡识别会更加精确），但是存在过拟合风险。3）太多隐藏层的网络可能会导致梯度消失难以训练。为了解决前两方面问题，通常使用卷积神经网络。为了解决第3个问题，通常使用残差神经网络。下面我们用一个9网格点的流场数据来解释卷积神经网络的计算流程。

单通道CNN

如下图所示，首先假定我们要处理的是一个9网格点的流场。这个流场仅仅存在\(u\)速度，其他的速度都是0。这样会使问题大大简化。每个网格点上对应的速度分量如图显示。卷积神经网络首先需要定义卷积核。就是下图中的\(k\)的4个值（这代表一个卷积核）。卷积核从数学上很好理解。加入把\(k\)卷积核应用到9网格点的流场数据上，会输出右侧4网格点的流场数据。其中的计算公式如下：

(1)\[ a_1=u_1k^u_1 + u_2k^u_2 + u_3k^u_3 + u_4k^u_4 \]

(2)\[ a_2=u_2k^u_1 + u_3k^u_2 + u_5k^u_3 + u_6k^u_4 \]

(3)\[ a_3=u_4k^u_1 + u_5k^u_2 + u_7k^u_3 + u_8k^u_4 \]

(4)\[ a_4=u_5k^u_1 + u_6k^u_2 + u_8k^u_3 + u_9k^u_4 \]

卷积核有点类似探照灯的作用，首先其照亮\(u_1,u_2,u_4,u_5\)网格点，进行数学操作，得到一个值。其次卷积核向右移动一个网格单元。照亮\(u_2,u_3,u_5,u_6\)网格点，进行数学操作，得到一个值。然后向下移动一个网格单元，从左边继续照。一直从左上方扫描到右下脚，卷积核就完成了这个操作。相应的会组建出\(a\)值。这一系列\(a\)的值，要比原始的9网格点的数据要少。下图取自另外一个连接。其也表示了卷积核的数学操作。

(5)\[\begin{split} \begin{split}0\times0+1\times1+3\times2+4\times3=19,\\ 1\times0+2\times1+4\times2+5\times3=25,\\ 3\times0+4\times1+6\times2+7\times3=37,\\ 4\times0+5\times1+7\times2+8\times3=43.\end{split} \end{split}\]

在这里其实已经包含了一些卷积神经网络的概念。我们可以将卷积核一次向右1个网格单元，也可以向右移动2个网格单元。这个具体的值，叫做步幅（stride）。同时，我们的卷积核为\(2\times 2\)，也就是说卷积核的大小为4。

双通道CNN

考虑下图，下图中添加了\(v\)方向的速度。这样就构成了2个通道。如果每个网格点上存在2个变量，也即2个通道。其可以理解为输入的变量是2个。一个是\(u\)，一个是\(v\)。那么后面每一层的每一个神经元，对应的卷积核的数量也要是2个。也即\(k^u\)对应\(u\)的卷积，\(k^v\)对应\(v\)的卷积。

卷积核在工作的时候，针对\(u\)和\(v\)都是进行相同的操作，最终会输出\(a_1,...,a_4\)，以及\(b_1,...,b_4\)，最终的结果要把\(a\)与\(b\)的值相加，得到一个\(c\)，上图只有一个神经元。

下图取自另外一个连接。其表示了一个具体的多通道卷积操作的计算流程。单通道指的是每个网格上只有一个变量，多通道指的是每个网格上存在多个变量。

一般情况下，要使用多个神经元。在2个通道下，每个神经元具有2个卷积核。在下图中就表示了针对每个速度分量，使用了5套不同卷积核（2个速度分量，因此一共10个卷积核）组成的卷积网络的第一层。图中的黑点表示神经元。当然了，在进行卷积操作之后还需要进行激活。在这里可以简单的使用ReLU函数做激活。下图中的5个黑点，构成了第1层卷积层。

上图中最后一列神经元对应的网格数量已经很少（是一个\(4\times 4\)的网格），因此没必要附加更多层。

在下图中，假定经过第1个卷积层之后，每个神经元输入的还是多行多列的数据，在这种情况下，可以再附加一层卷积层。下图中我们在第1层卷积层布置了5个神经元，第2层卷积层具有2个神经元。因此一共有2套卷积核，每套卷积核里面有5个卷积核，因此一共10个卷积核。

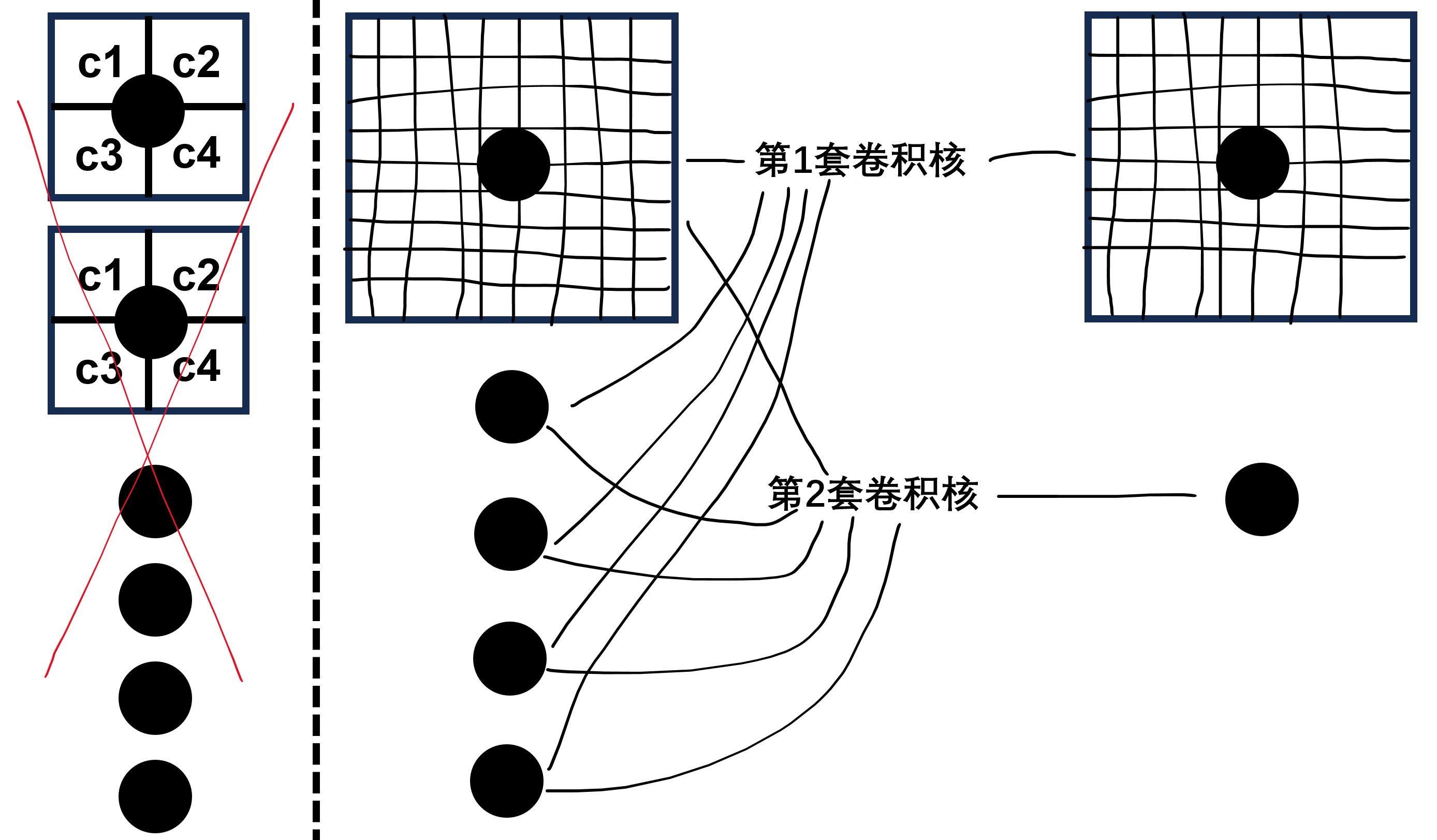
同时也可以看出，在卷积神经网络的卷积层里，之前全连接网格的未知参数权重，被替换成了卷积核内的参数\(k\)。下图是一个更细化的卷积网络示意图。首先我们有一个\(8\times 8\)的网格系统，其中的速度具有2个分量，因此其可以认为具有2个通道。在这种情况下，每个网格点定义一个\(u\)和\(v\)，因此一共共有128个数值需要读取到输入层。如果输入层后面直接对接全连接网格的隐藏层，加入调用8个神经元。那么未知的权重数量为\(128\times 8=1024\)个（在这里还没有考虑偏置）。

下面来看卷积神经网络。上图中的128个数值，如果对接的是5个神经元的卷积层，那么每个神经元对应的卷积核有4个未知值，因为具有2个通道，因此每个神经元对应了8个未知的值。一共5个神经元，因此未知的卷积核权重\(k\)共有\(4\times 2\times 5=40\)个。同时，因为使用的是\(2\times 2\)卷积核，因此这一层的每个神经元的数据变成了\(6\times 6\)，因为有5个神经元，则总共进入到这一层的数据一共有\(6\times 6\times 5=180\)个。

然后进入到下一层，下一层假定同样调用5个神经元，那么未知的卷积核权重\(k\)共有\(4\times 5\times 5=100\)个。同样的因为使用的是\(2\times 2\)卷积核，因此这一层的输入数据变成了\(4\times 4\times 5=80\)个。在下一层，通常会附加一个最大池化的操作。下图取自另外一个连接。其表示了最大池化的过程。很简单，最大池化类似一种糙化过程。输入4个数进去，最大池化会输出1个最大的值。因此对于本算例，在第2层句卷积层上，因为每个神经元处理的就是\(4\times 4\)网格，因此最大池化后仅仅剩下一个数值。因此在最大池化层的值只有5个值。

随后可以进行进一步的卷积操作。但是本算例已经处理到最小。因此后面可直接附加全连接层。本算例将最大池化后的所有值进行展平成列向量作为全连接的输入层。最后附加全连接的隐藏层。隐藏层存在8个神经元。因此隐藏层共存在\(8\times 5=40\)个位置权重。

至此可以看一下卷积网络的未知权重个数。首先第一层卷积层未知权重为40个，第二层未知权重为100个。全连接隐藏层未知权重为40个。总共180个权重。大大少于不使用卷积神经网络的1024个权重值。

卷积神经网络的训练过程，与全连接网络相同，均需要使用后向传播来进行。可参考ML: 手算反向传播与自动微分。

一些结果

下图是一个在OpenFOAM环境下，通过libtorch的maxpooling函数做的4次最大池化的效果。很明显，最大池化保留了原有顶盖驱动流的流动特征。注意，下图在左下角有一个多孔介质方块区域，这个方块内的速度较小。

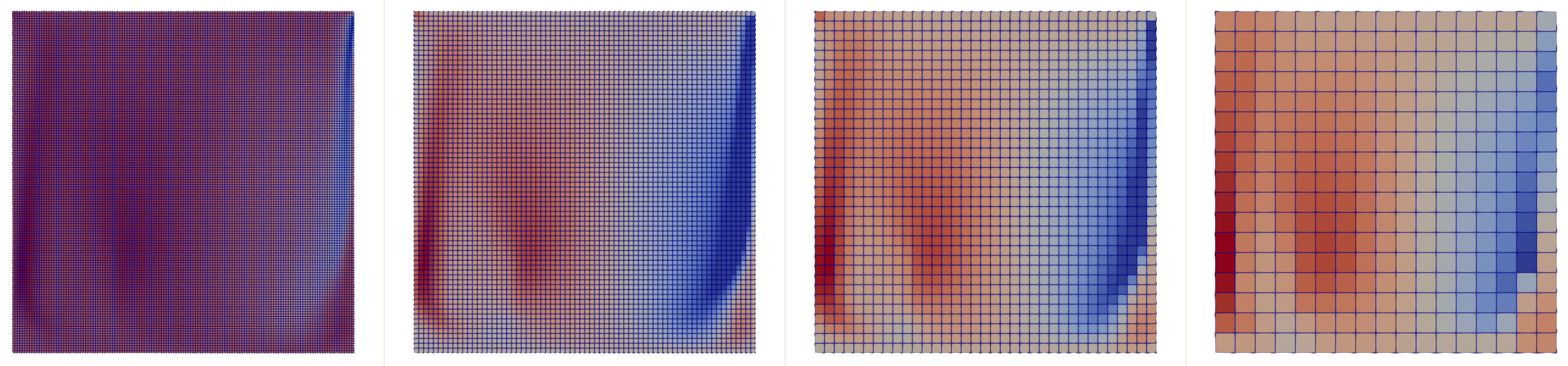
下图是通过libtorch的conv2D函数，输入2通道（分别是\(x\)方向速度以及\(y\)方向速度）并输出5通道的流场结果。注意，下图在左下角有一个多孔介质方块区域，这个方块内的速度较小。

下图是通过下列代码执行一系列的卷积、池化操作等输出的8个通道的流场结果：

net_ = register_module
(
    "net", 
    torch::nn::Sequential
    (
        torch::nn::Conv2d(2, 5, 3),
        torch::nn::BatchNorm2d(5),
        torch::nn::Tanh(),
        torch::nn::MaxPool2d(2),
        torch::nn::Conv2d(5, 10, 3),
        torch::nn::BatchNorm2d(10),
        torch::nn::Tanh(),
        torch::nn::MaxPool2d(2),
        torch::nn::Conv2d(10, 10, 3),
        torch::nn::BatchNorm2d(10),
        torch::nn::Tanh(),
        torch::nn::MaxPool2d(2),
        torch::nn::Conv2d(10, 8, 3),
        torch::nn::BatchNorm2d(8),
        torch::nn::Tanh(),
        torch::nn::MaxPool2d(2)
    )
);

[BFM19]

A. Beck, D. Flad, and C. Munz. Deep neural networks for data-driven LES closure models. Journal of Computational Physics, 398:108910, 2019.

[GLI16]

X. Guo, W. Li, and F. Iorio. Convolutional neural networks for steady flow approximation. In Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining, 481–490. 2016.

[HZRS16]

K. He, X. Zhang, S. Ren, and J. Sun. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, 770–778. 2016.

[LBD+89]

Y. LeCun, B. Boser, J.S. Denker, D. Henderson, R.E. Howard, W. Hubbard, and L.D. Jackel. Backpropagation applied to handwritten zip code recognition. Neural computation, 1:541–551, 1989.

[LBBH98]

Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86:2278–2324, 1998.

[SJSK19]

V. Sekar, Q. Jiang, C. Shu, and B.C. Khoo. Fast flow field prediction over airfoils using deep learning approach. Physics of Fluids, 2019.