版本对应：

本网页讨论的机器学习内容，为特定的机器学习内容（并未与CFD结合）。在《无痛苦NS方程笔记》中， 特定的将CFD与机器学习互相结合起来，无普适性机器学习内容。

ML: 自编码器和Unet

在阅读本文之前，请先阅读ML: 卷积神经网络。

自编码器（autoencoder）可以理解为编码器（encoder）与解码器（decoder）的组合。在机器学习领域，自编码器主要用于输入一个图形，然后输出一个压缩的或重组的近似的图像。自编码器可以理解为一种数据压缩/重构算法。编码器主要用于数据压缩，解码器主要用于从压缩的数据进行重构。在训练自编码器的过程中，最小化输入数据与重构数据之间的误差，从而调使得编码器能够有效地压缩输入数据，解码器能够准确地从压缩的数据中进行重构。

自编码器具有一些特征：

  • 数据定向性：比如如果训练的自编码器可以用来压缩数字图像，那就只能对数字进行压缩，而不能对食物进行压缩；

  • 存在失真：压缩（重构）后的图像存在失真。如下图所示；

_images/output_s4LlDOS6FUA1_0.png

由于自编码器的数据定向性，目前并没有大量的使用自编码器来进行图像压缩。但目前自编码器大量的被用于图像降噪以及异常识别。例如在下图中，将下图自编码器预测的图像，与输入图像相对比。很明显其差异可以作为异常。因此自编码器也可以用来预测异常数据。

_images/output_sfxr9NdBCP_x_0.png

同时注意：编码器与解码器是一类统称。例如两层神经网络的结构，可以把第一层当做编码器，第二层当做解码器。其也不限定为必须为卷积网络，全连接网络也可以。例如在这个链接中，就是采用的2层全连接网络做的自编码器来识别数字。

下面是在OpenFOAM环境下，挂载libtorch，采用卷积层、Tanh激活层、Bilinear上采样制作的自编码器针对19600网格点的顶盖驱动流进行的流场重组（每训练100次出一张图）。很明显，经过训练的推进，流场越来越趋向于CFD的结果。

_images/cnnreal.JPG

CFD流场重构

自编码器以及其变种可以用于图像重构，也可以用于CFD的流场重构。

在CFD领域，一些研究通过Unet进行流场重构预测。Unet是一个2015年被提出来的神经网络结构[RFB15]。最初用于医学领域的图像分割（image segmentation）。其主要特点是其是一个对称的、全卷积网络。原生的Unet后面会详细介绍。

另一方面，在ML: 卷积神经网络中，通过一系列的卷积、激活、以及池化层后，数据大量的减少。其也可以理解为一种编码器。因此，CFD领域的编码器在本文不做介绍，可以直接参考ML: 卷积神经网络。

在将流场数据进行编码后，会发现数据大量的被压缩，在附加卷积操作后图形特征也会变化。解码器的主要目的就是给定一个经过编码器处理的数据，将其还原成原本的流场信息的工具。在编码器工作的时候，需要调用卷积、激活、以及最大池化（下采样）。解码器可以理解为编码器的反向操作。最简单的解码器就是图像识别里面的softmax函数，其对各种图像进行分类。在CFD流场重建领域，不能使用softmax函数。在流场重建领域的解码器工作时，需要调用转置卷积（反卷积）、激活、以及上采样（可以理解为反向最大池化）。很明显，编码器与解码器可以看做是一种正向与反向操作。

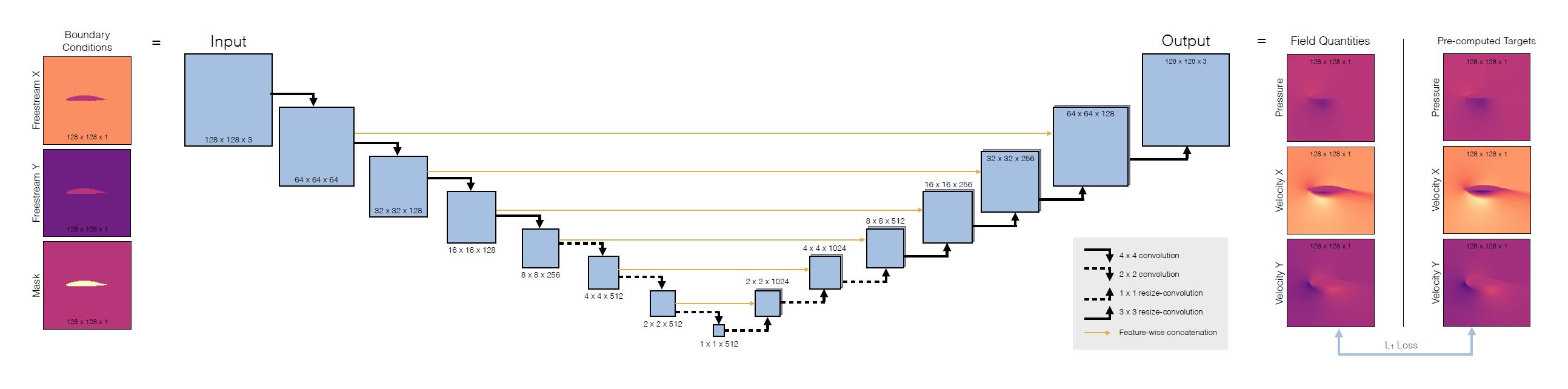
_images/unet.jpg

上图是一个采用类似Unet结构对流场进行重构的示意图[TWeissenowPH20]。在这个特定的Unet变种中，其也是一个对称的结构，同时采用了跳跃连接的方式来进行，其有助于解决传统编码器中的信息丢失和梯度消失问题。更详细的信息可以参考ML: 残差神经网络。同时其也是一个全卷积网络。这是一个典型的使用通过编码器与解码器、附加跳跃连接构建的Unet来实现流场重构的典型方法。

下文介绍典型的解码器常用的转置卷积以及上采样操作。最后对Unet做总结。

Warning

一些文章把自编码器解释为无监督学习。但Keras博客表示自编码器并不是一个完全的无监督学习。自编码器更像是自监督学习，其标签是通过输入数据产生的。

转置卷积

在ML: 卷积神经网络中介绍了卷积的操作。其更形象的可以参考下图。下图是一个\(2\times 2\)卷积核对\(4\times 4\)网格的扫描操作。其中下部分网格是输入，上部分网格是输出。

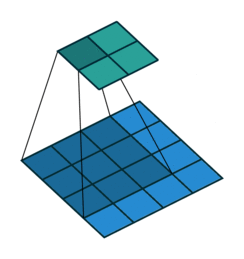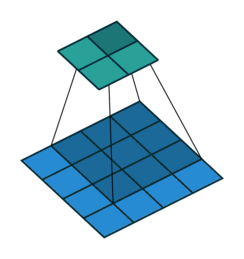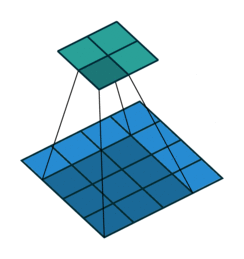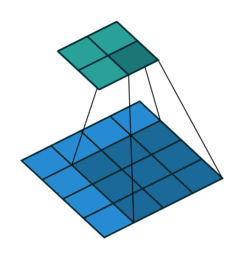
_images/no_padding_no_strides.gif

类似上图，下图是一个\(3\times 3\)卷积核对\(5\times 5\)网格进行转置卷积的操作。其中上部分网格是输入，下部分网格是输出。

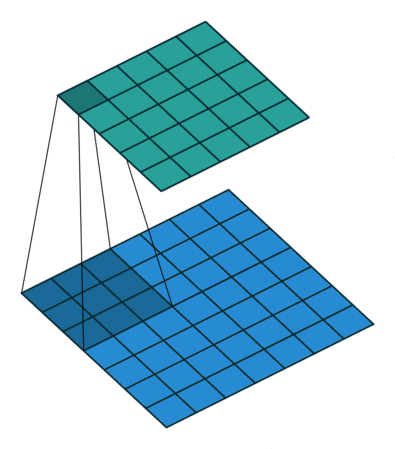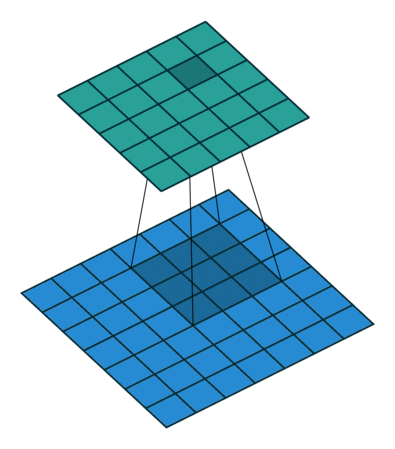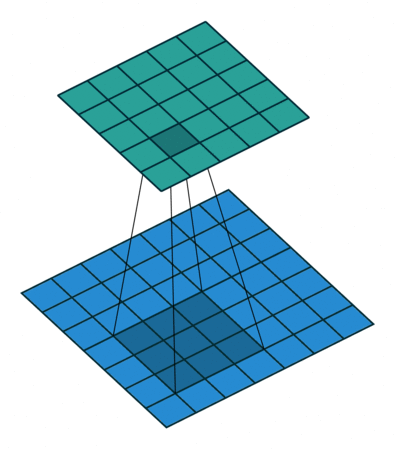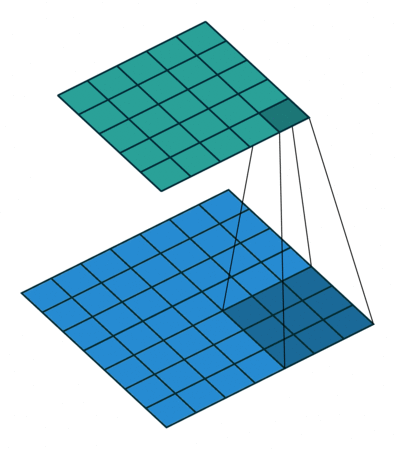
_images/full_padding_no_strides_transposed.gif

其计算原理可以参考下图：

_images/trans_conv.svg

以上图中output的第4几个结果为例，其0、3、6、9就是简单的通过下列方程计算而来：

(1)\[\begin{split} 0=3 \times 0 \\\\ 3=3 \times 1 \\\\ 6=3 \times 2 \\\\ 9=3 \times 3 \end{split}\]

上图中简单的调用了一个\(2\times 2\)卷积核，将一个\(2\times 2\)的输入，变成了\(3\times 3\)的输出。如果继续调用其他的卷积核。则可以变成多个\(3\times 3\)的输出。也即构成了多通道转置卷积。

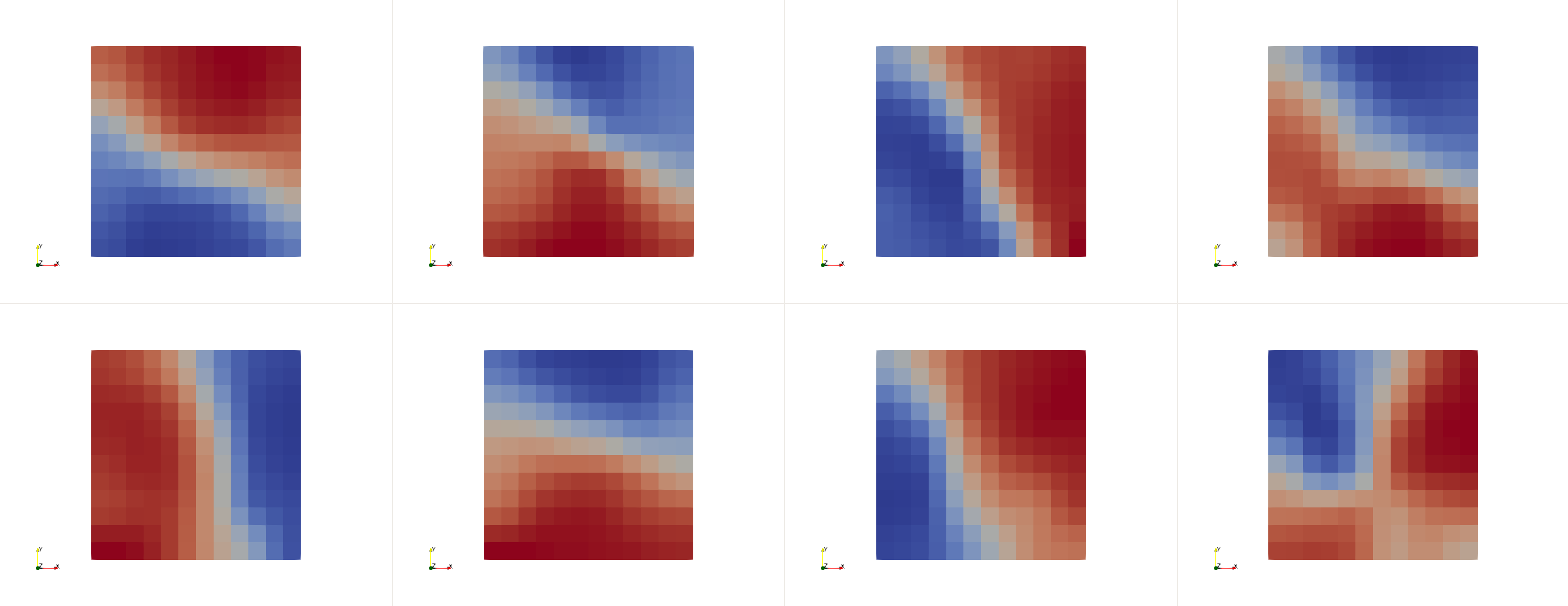
同样注意，转置卷积操作可能会导致棋盘分布。例如对于ML: 卷积神经网络中通过libtorch的conv2D函数，执行一系列的卷积、池化操作等输出的8个通道的流场结果后，再进行转置卷积后则呈现下图的棋盘分布。

_images/cnncavity4.png

上采样

上采样可以理解为最大池化的反向操作。上采样有很多不同的方法，在这里介绍最简单的方法。

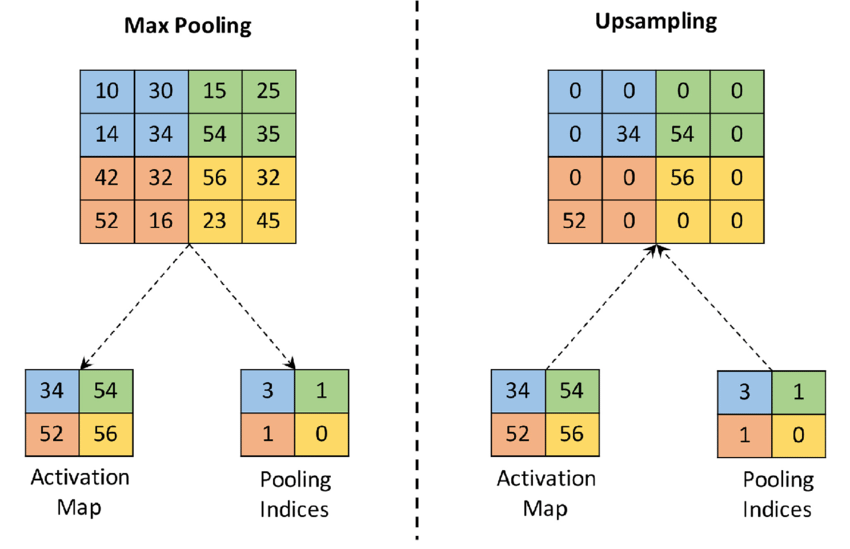
_images/upsampling.png

在上图中，左图为针对\(4\times 4\)网格所做的最大池化。其进行池化操作的过程，会记住每次池化操作的最大元素的位置信息。反过来在进行上采样的过程时，简单的把最大数值按照最大元素位置进行填充，其他元素置为0即完成了上采样的操作。

类似上图，如果将转置卷积改成上采样方法，棋盘分布消失：

_images/cnncavity5.png

Unet

Unet与自编码器最重要的区别就是Unet使用了跳跃连接，同时Unet需要调用标签。下图是Unet的典型应用。其输入一个真实的图像，可以把相关的mask进行输出。

_images/imgse.JPG

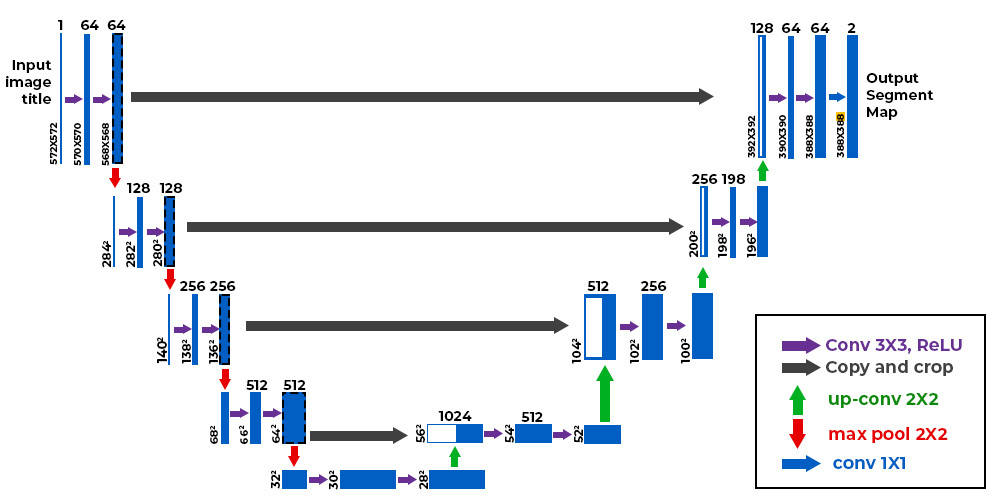
_images/Group14.jpg

上图是原生Unet的网络设计[RFB15]。在这里将其按步骤进行解释，首先是编码器：

  1. 首先输入数据是\(572 \times 572\)的像素图；

  2. 进行卷积操作，形成\(64\times 570 \times 570\)的tensor，其中64表示通道数；

  3. 进行卷积操作，形成\(64\times 568 \times 568\)的tensor；

  4. 进行最大池化，形成\(64\times 284 \times 284\)的tensor；

  5. 进行卷积操作，形成\(128\times 282 \times 282\)的tensor；

  6. 进行卷积操作，形成\(128\times 280 \times 280\)的tensor；

  7. 进行最大池化，形成\(128\times 140 \times 140\)的tensor；

  8. 进行卷积操作，形成\(256\times 138 \times 138\)的tensor；

  9. 进行卷积操作，形成\(256\times 136 \times 136\)的tensor；

  10. 进行最大池化，形成\(256\times 68 \times 68\)的tensor；

  11. 进行卷积操作，形成\(512\times 66 \times 66\)的tensor；

  12. 进行卷积操作，形成\(512\times 64 \times 64\)的tensor；

  13. 进行最大池化，形成\(512\times 32 \times 32\)的tensor；

  14. 进行卷积操作，形成\(512\times 30 \times 30\)的tensor；

  15. 进行卷积操作，形成\(512\times 28 \times 28\)的tensor；

至此，编码器形成\(512\times 28 \times 28\)的tensor。下面进行解码器：

  1. 将编码器第12步形成的\(512\times 64 \times 64\)的tensor进行resize成为\(512\times 56 \times 56\)的tensor；将\(512\times 28 \times 28\)的tensor进行转置卷积形成\(512\times 56 \times 56\)的tensor。将两个tensor进行拼接，形成\(1024\times 56 \times 56\)的tensor；

  2. 将\(1024\times 56 \times 56\)的tensor进行卷积，形成\(512\times 54 \times 54\)的tensor；

  3. 将\(512\times 54 \times 54\)的tensor进行卷积，形成\(512\times 52 \times 52\)的tensor；

  4. 将\(512\times 52 \times 52\)的tensor进行转置卷积，形成\(512\times 104 \times 104\)的tensor。将编码器第9步形成的\(256\times 136 \times 136\)的tensor进行resize成为\(256\times 104 \times 104\)的tensor；将两个tensor进行拼接，形成\(512\times 104 \times 104\)的tensor；

  5. 将\(512\times 104 \times 104\)的tensor进行卷积操作，并以此类推…

Unet的神经网络看起来像一个U形状。因此被称之为Unet。其中的跳跃连接，使得Unet相对于自编码器不会过度的压缩与失真。

[RFB15] (1,2)

O. Ronneberger, P. Fischer, and T. Brox. U-net: Convolutional networks for biomedical image segmentation. In Medical image computing and computer-assisted intervention–MICCAI 2015: 18th international conference, Munich, Germany, October 5-9, 2015, proceedings, part III 18, 234–241. Springer, 2015.

[TWeissenowPH20]

N. Thuerey, K. Weißenow, L. Prantl, and X. Hu. Deep learning methods for Reynolds-averaged Navier–Stokes simulations of airfoil flows. AIAA Journal, 58:25–36, 2020.