ML: 死掉的神经元

在使用ReLU函数进行训练的时候，要注意死掉的神经元的产生。本文通过数学方程简介死掉的神经元的产生。

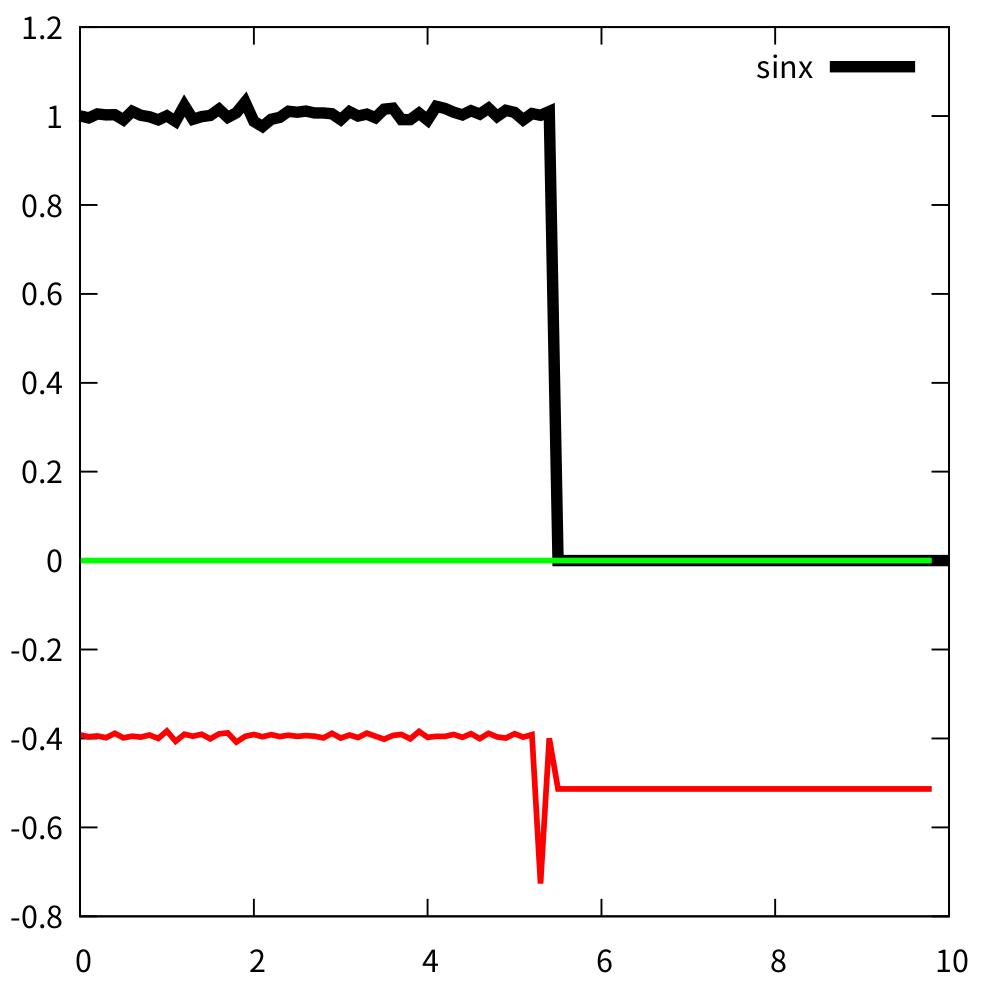
下图是使用卷积神经网络进行PDE间断识别的时候发生的一个情况。黑线表示输入的附加噪音的PDE黎曼解。红色为卷积层处理的单通道第一层数据。蓝线表示ReLU激活函数的输出数据。如果不了解卷积神经网络也没关系，主要问题最大的地方在于蓝线全部都是0。这可能会导致死掉的神经元的产生。

其根本在于，不管是卷积层，还是全连接层，预测的红线如果全部都是负值，那么ReLU的输出就都是0，这会带来很大问题。下面我们通过数学的形式来进行解释。

假定某一套神经网络，其输入层具有3个参数\(x_1,x_2,x_3\)，将其与一个神经元连接的时候，输入到神经元的数学形式为：

(1)\[ f(\mathbf{x})=w_1x_1+w_2x_2+w_3x_3+b \]

其中\(\mathbf{x}\)表示\(x_1,x_2,x_3\)。假定输入的是

(2)\[ x_1=10,x_2=11,x_3=12 \]

恰巧某一次我们的权重为：

dyfluid@dyfluid-virtual-machine:~/OKS202409/test$ cnnFoam
weights: (1,.,.) = 
 -0.14  0.3 -0.19

数学形式为：

(3)\[ w_1=-0.14,w_2=0.3,w_3=-0.19 \]

Warning

机器学习里面的权重可以是负值。

将方程(3)代入到(2)有：

(4)\[ f(\mathbf{x})=(-0.14\times10)+(0.3\times11)+(-0.19\times12)=-0.38 \]

很明显-0.38小于0。在将其输入到ReLU函数的时候：

(5)\[ \mathrm{ReLU}(f(\mathbf{x}))=\max (-0.38,0)=0 \]

激活后变成了0。ReLU激活函数在输出是0的时候，其导数计算也是0，后续在进行反向传播的时候，无法用来更新梯度以及权重。权重就被锁定到\(w_1=-0.14,w_2=0.3,w_3=-0.19\)。损失也不会继续下降，导致训练失败。

复活的神经元

那么死掉的神经元能否复活？在大部分情况下是可以的。首先，方程(5)输入的仅仅是\(x_1,x_2,x_3\)，仅仅有3个值。实际情况可能会有1000个值。将这1000个值做卷积层，经过卷积核操作之后，假定卷积核的大小是3，每次移动1个步幅，其能输出998个值。在这1000个数值中，取\(x_1,x_2,x_3\)可能会导致\(\mathrm{ReLU}(f(\mathbf{x}))<0\)，但取\(x_2,x_3,x_3\)可能不会。所以\(\mathrm{ReLU}(f(\mathbf{x}))\)必然有大于0的时候。虽然这种情况下，卷积网络处理的数据输出会大量失真。

大量失真是应为只使用了1个卷积核，只有3个权重。这在实际情况中是基本不可能的。如果使用10个或者更多的卷积通道，情况就会不一样。下图中使用了10个卷积通道。可见，还是会有一些红线掉到了0以下，这些卷积神经元可能就死了。但同时还有其他几个活着的神经元。因此，卷积网络使用多个通道，可以避免死掉的神经元。

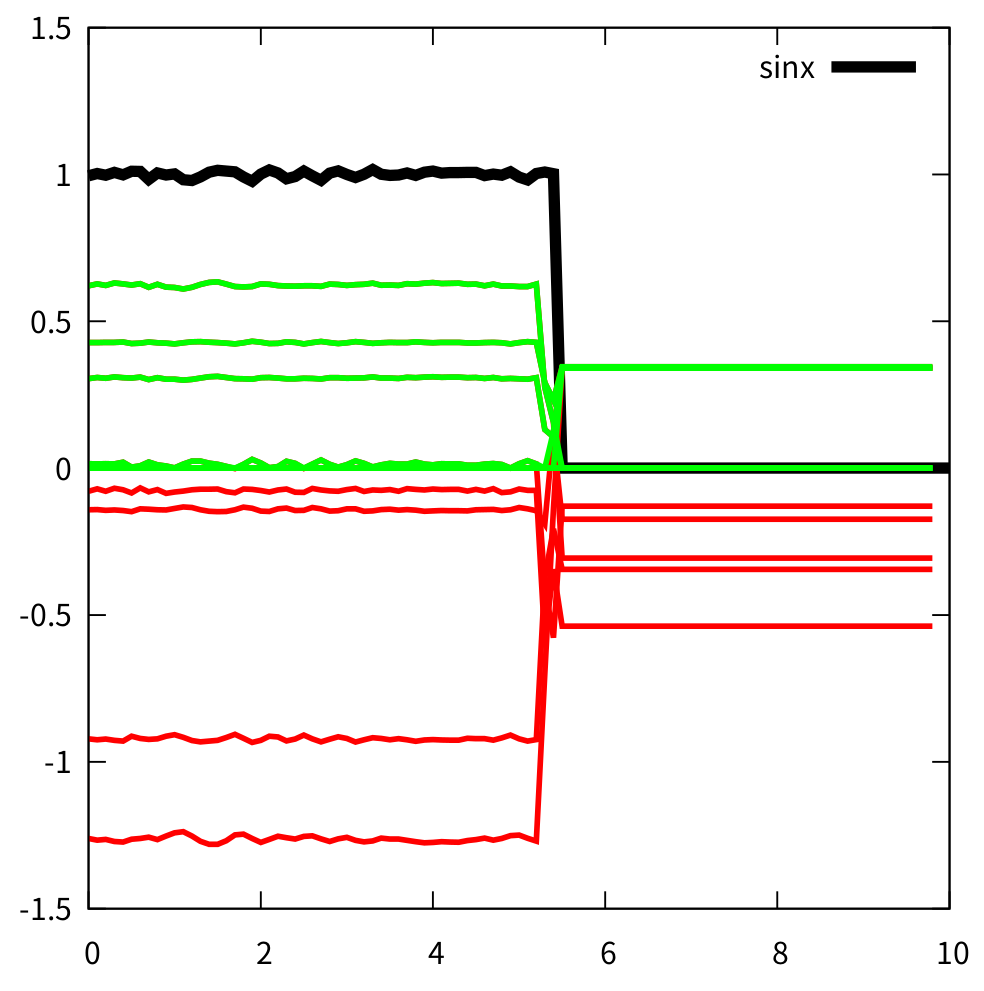
另外，真正能使得神经元复活的，是批次的使用。在训练的过程中，这1000个数据只能构成一个批次。如果进行PDE间断的捕获，要输入很多的批次。即使这个批次的神经元死了一些。换下一个批次的数据，可能又会复活。

还有一些其他方法可以处理神经元的死亡问题。比如也可以吧输入进行归一化处理，使用非ReLU函数等。